La Relativité restreinte ne considère que des corps animés d’une vitesse uniforme les uns par rapport aux autres. Albert Einstein a poursuivi sa théorie géniale en considérant tous les mouvements possibles, c’est-à-dire en prenant en compte des mouvements accélérés.

Dans le billet précédent  1 – Le principe d’équivalence , dans une de ses fameuses expériences de pensée, Einstein imagine un passager dans une cabine galactique, loin de tout, tractée par une corde géante avec une force F qui lui confère une accélération γ.

Il conclut qu’être soumis à cette accélération ou à un champ de gravitation g = γ est équivalent.

Si l’accélération courbe la lumière …

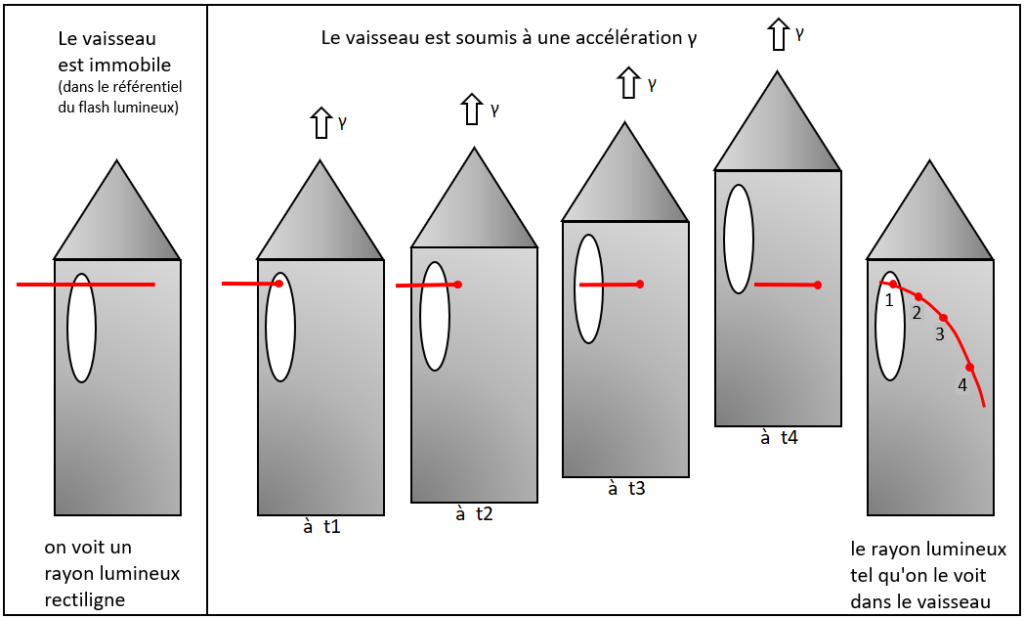
Faisons maintenant une expérience de pensée analogue, et considérons le cas d’un flash lumineux émis dans le vide galactique et se propageant tout droit. Ce flash entre par un hublot de la cabine d’un vaisseau. Si le vaisseau est immobile (par rapport au référentiel d’où est tiré le flash lumineux), le passager verra un rayon lumineux rectiligne. Mais qu’en sera-t-il si le vaisseau est en accélération, donc avec une vitesse croissante ?

A des instants t1, t2, t3 et t4 espacés de façon régulière, les distances parcourues par le vaisseau sont croissantes puisqu’il accélère. Les points de l’espace atteints successivement  par le rayon lumineux en t1, t2, t3 puis t4 sont donc de plus en plus bas dans la cabine, comme le montre le dessin. Le passager verra alors le rayon lumineux courbé vers le bas, ce qu’il attribuera logiquement à son accélération.

Mais avec le principe d’équivalence, si l’accélération courbe la lumière, alors la gravitation la courbe aussi !

… alors la gravitation la courbe aussi

Or la gravitation – une masse qui en attire une autre – n’est pas censée agir sur la lumière, qui est justement dépourvue de masse. Comment un objet massif peut-il donc courber la lumière ?

Einstein mettra des années à le comprendre et expliquera en 1915 qu’en fait ce n’est pas le trajet de la lumière dans l’espace qui est courbé, mais l’espace lui-même ! La lumière emprunte le plus court chemin d’un espace courbé, tout comme le plus court chemin sur terre entre deux points est une courbe, liée à la rotondité de la terre.

La Relativité restreinte avait apporté la notion d’espace-temps (1). La Relativité générale nous dit que la gravitation n’est pas un champ de force mystérieuse dans notre espace tridimensionnel. C’est une propriété géométrique de notre espace-temps, qui a des caractéristiques géométriques bien à lui dépendant de la distribution des masses (étoiles, planètes, trous noirs …).

Einstein a  publié une équation qui décrit comment la matière modifie la géométrie de l’espace-temps. La masse est la propriété de cette matière à déformer plus ou moins l’espace-temps, qui est interprétée comme son champ gravitationnel. Le mouvement d’un corps dans ce champ gravitationnel, son trajet, est décrit très précisément par le calcul.

Le temps se dilate aussi

Einstein a aussi montré que, puisqu’un objet massif courbe l’espace-temps en le dilatant, il dilate aussi le temps par rapport à un temps mesuré à distance de la déformation: si deux horloges identiques sont placées l’une dans un fort champ de gravitation, l’autre loin de ce champ, alors on constatera que la première retarde par rapport à l’autre. La gravitation, donc la proximité d’une masse, dilate le temps local. A ne pas confondre avec la dilatation du temps propre en relativité restreinte (1).

Cet effet a été mesuré avec une extrême précision. On a par exemple installé deux horloges atomiques à des altitudes différents, donc soumises à une gravitation différente puisque celle-ci augmente en se rapprochant du centre de la terre. Le résultat confirme de façon parfaite la théorie . Le génie d’Einstein est d’avoir compris cet effet très jeune, et à l’époque sans aucune possibilité de vérification expérimentale puisque les horloges atomiques n’existaient pas encore.

–oo–oo–

1. Voir le billet Relativité restreinte – 1 L’espace-temps