Petit, j’ai vraiment compris comment on additionnait des fractions quand on me l’a expliqué avec des tartes…

D’abord une fraction, comme son nom l’indique, c’est une partie de quelque chose. Par exemple une part de tarte, un quart ou une demi-tarte.

Maintenant, si on veut additionner un quart plus une demi-tarte, le problème c’est que un quart ou un demi sont des choses différentes qu’on ne peut pas additionner, pas plus qu’on ne peut additionner des carottes avec des salades, même si ce sont tous des légumes !

Mais si on dessine ces morceaux de tarte, on voit bien l’astuce en remarquant qu’une demi-tarte est égale à 2 quarts, ce qui permet d’ajouter un quart à deux quarts, soit 3 quarts et le tour est joué.

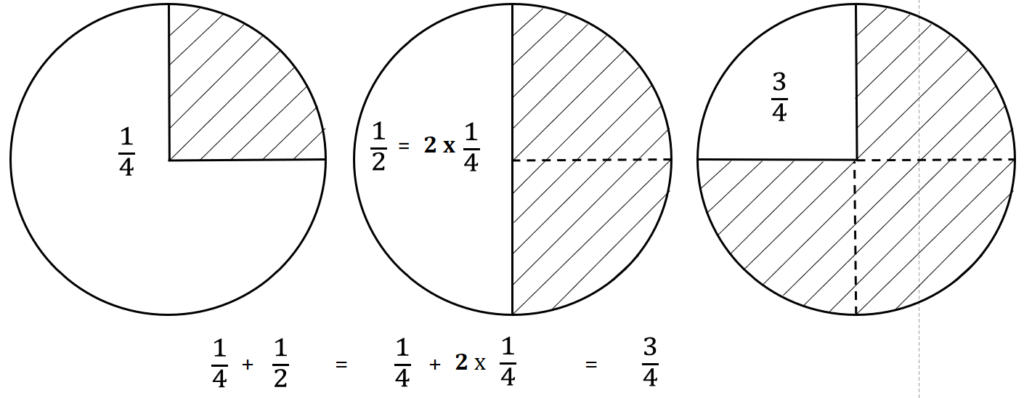
Maintenant si on additionne deux fractions moins simples, par exemple 1 quart et 1 tiers,  qu’est-ce que ça donne ?

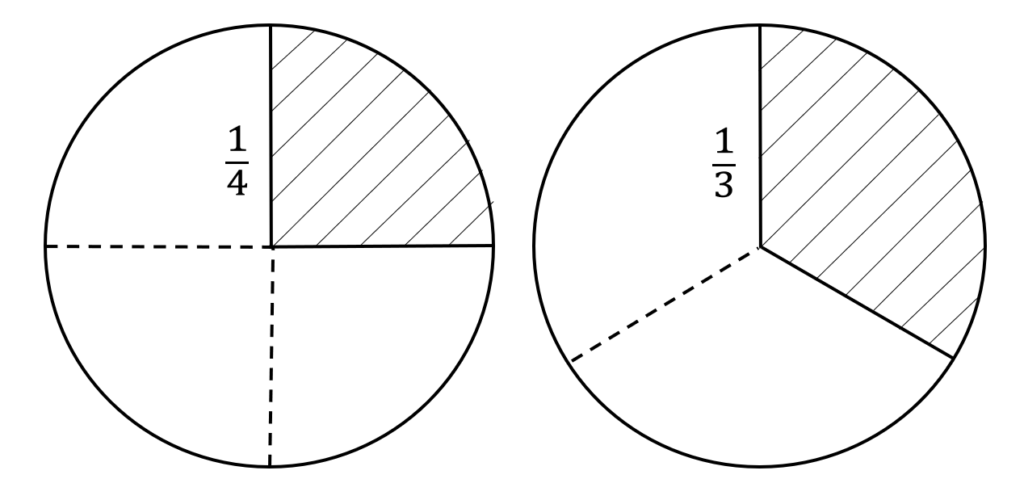
Passons à nouveau par des tartes… Pour faire cela, on va se débrouiller pour couper la tarte des deux côtés en morceaux de même taille, qu’on pourra donc additionner. Ici ça marche en découpant les tartes en petits  douzièmes ; on verra plus loin pourquoi.

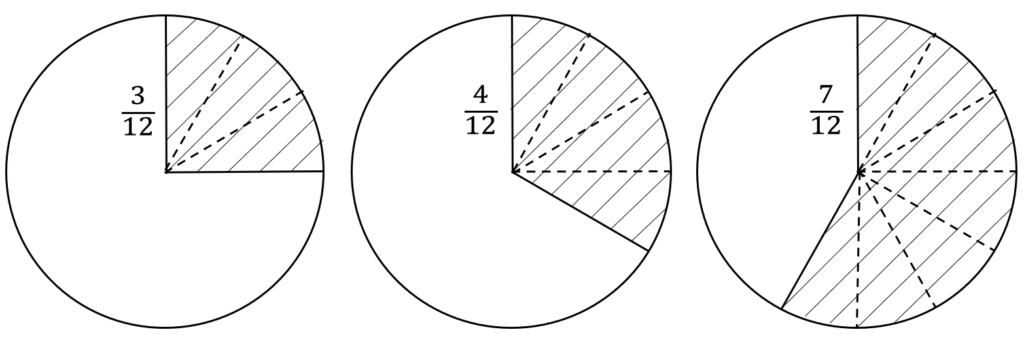
On a donc d’un côté un quart ou 3 douzièmes de tarte, et de l’autre un tiers ou 4 douzièmes de tarte. On peut alors ajouter des douzièmes à d’autres douzièmes, ce qui nous fait :

4  +  3 douzièmes = 7 douzièmes

En résumé : 

 \frac{1}{4} + \frac{1}{3} = \frac{3}{12} + \frac{4}{12} = \frac{7}{12}

Pour aller plus loin

On appelle les deux nombres constituant la fraction le « numérateur » en haut et le « dénominateur » en bas 

 7  (numérateur)

12 (dénominateur)

Le dénominateur « dénomme », ce qui veut dire qu’il donne un nom à ce qu’on veut additionner, ici des douzièmes de tarte. Le numérateur, lui, va compter ces douzièmes, ici 3 et 4, puis 7.

On a vu que pour ajouter des fractions, il faut découper les tartes en plus petits morceaux de taille égale de part et d’autre. On dit qu’il faut trouver un dénominateur commun, ici 12, des douzièmes de tarte.

Une façon sûre de le trouver est de multiplier les deux dénominateurs des fractions à additionner entre eux, soit 

4 x 3 = 12

On peut aussi aller plus loin et soustraire des fractions de cette façon. Par exemple pour faire 1 tiers de tarte moins un quart de tarte, on va aussi tout couper en douzièmes de tarte, et il restera à la fin :

 \frac{1}{3} - \frac{1}{4} = \frac{4}{12} - \frac{3}{12} = \frac{1}{12}

–oo–oo–