
On rappelle le billet précèdent : dans un repère Galiléen, un corps qui n’est soumis à aucune force sera immobile ou animé d’un mouvement rectiligne à vitesse constante, c’est la première loi de Newton. Pour que ce corps décrive une courbe, une trajectoire circulaire par exemple, il faut nécessairement qu’une force l’y contraigne, qu’elle l’empêche d’aller tout droit… En faisant tournoyer une fronde, je sens bien que je dois retenir le corps en rotation, c’est la force « centripète ».
Je suis maintenant assis dans une voiture qui tourne. Dans un référentiel Galiléen une force radiale centripète lui est appliquée. Si je change de référentiel, celui attaché à la voiture qui tourne, donc non Galiléen, où les lois de Newton ne s’appliquent pas, ma perception est tout autre. J’ai l’impression en réalité qu’une force « centrifuge » tend à me projeter hors de la voiture.
Comme il est plus simple et plus naturel de raisonner dans ce référentiel tournant non Galiléen, les physiciens ont inventé cette pseudo-force centrifuge qui permet quand même d’appliquer les lois de Newton. Je dirai alors : dans le référentiel tournant de ma voiture, je suis soumis à une pseudo-force centrifuge et à une réaction opposée des parois, la force centripète. Ces 2 forces égales et opposées s’annulent, et donc je suis bien immobile par rapport à la voiture.
Force centripète = – Force centrifuge = m . V² / R = m . ω² . R
Le passage d’un repère Galiléen à un repère tournant n’est pas neutre en physique. Il implique la prise en compte d’une pseudo-force centrifuge, résultant de la rotation du repère.
Chaises volantes
Avec l’exemple des chaises volantes , on introduit le poids du corps.

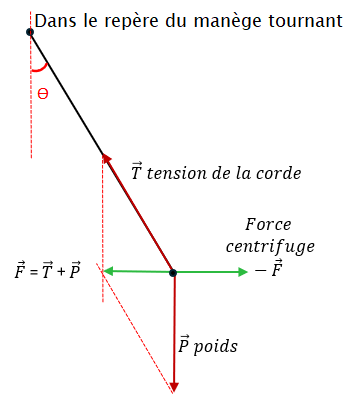
L’angle ϴ des suspentes de la chaise s’adapte pour que la somme des forces (centrifuge + poids + tension des cordes) soit nulle, ce qui correspond bien à une chaise immobile, attention dans le repère tournant.
Plus la vitesse de rotation augmente, plus la force centrifuge augmente également, et donc l’angle ϴ. A grande vitesse, les suspentes sont presque horizontales, on retrouve une fronde.
–oo–oo–