
Je revois mon professeur de physique arriver en classe un matin, et nous parler du décollage réussi d’une des fusées du programme Apollo. Nous avions 16 ou 17 ans, et cela nous passionnait. Il nous propose de calculer la « vitesse de libération » nécessaire pour que la fusée s’échappe de l’attraction terrestre.
Je me souviens encore de mon étonnement devant la simplicité de l’exercice, et du plaisir de comprendre ce qui semblait auparavant trop complexe. Quand même, savoir calculer la vitesse de libération de la fusée !
Travail d’une force …
On sait que le travail d’une force appliquée à un corps représente l’énergie fournie par la force à ce corps. Ce travail est le produit de la force par le chemin qu’elle parcourt. Il est égal à la variation de l’énergie cinétique de ce corps, soit dans le cas simplifié d’un corps au repos à qui on applique une force F sur une longueur L :
F . L = 1/2 m.v²
où
- m = masse du corps
- v = vitesse atteinte par le corps
… appliqué à une fusée
Une fusée est soumise à la force d’attraction de la terre, c’est-à-dire son poids, qui dépend de son altitude et est égal à (loi de la gravitation universelle de Newton) :
P = G . M . m / D²
où
- G = constante gravitationnelle
- M = masse de la terre
- m = masse de la fusée, supposée ici constante
- D = distance du centre de la terre à la fusée
Lorsqu’une fusée quitte la terre, elle accélère et augmente sa vitesse jusqu’à échapper à l’attraction terrestre. Loin de la terre, on va dire à l’infini lorsqu’il n’y a plus d’attraction, elle a acquis un vitesse de libération V et une énergie cinétique Ec = ½ x m V² .
La fusée est soumise à son poids P, dont le travail depuis le sol, soit à D = R rayon de la terre, jusqu’à l’infini est égal à :
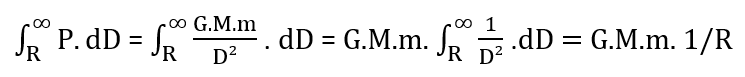
Ce travail est égal comme on l’a vu à l’énergie cinétique, d’où :
G . M . m . 1/R = ½ m . V²
V² = 2 G . M / R
Vitesse de libération de la fusée = \sqrt{2GM/R}
Calculons cette vitesse sur terre:
- R = 6,367 . 10^6 m
- G = 6,674 . 10^{-11} en unités internationales
- M = 5,972 . 10^{24} kg
On obtient, calculs faits : V = 11,2 km/s (1)

Voilà, c’est aussi simple que ça. Cette vitesse de libération ne dépend pas de la masse de la fusée, elle ne dépend que des caractéristiques de la terre, masse et rayon. Plus l’astre est massif, plus il attire. Sur la lune par exemple, la vitesse de libération est plus faible, V = 2,4 km/s.
On a vu dans le billet précèdent que la vitesse de satellisation est égale à \sqrt{GM/R} soit \sqrt{2} fois moins. Il s’agit là de mettre en orbite un satellite qui reste soumis à l’attraction terrestre.
Avec sa vitesse de libération, la fusée va échapper complétement à l’attraction terrestre.
–oo–oo–
- En réalité s’ajoute à la vitesse propre de la fusée celle de la terre, suivant la façon dont elle est lancée, pour profiter plus ou moins de l’effet de fronde. Cette vitesse additionnelle est cependant faible, inférieure au maximum de 0,465 km/s.