Dans les années 1960-1970, des travaux de plusieurs scientifiques inspirent Arthur C. Clark, auteur de science-fiction, qui publie le roman Les fontaines du paradis, dans lequel est popularisé l’idée d’un ascenseur spatial. C’est une sorte de gigantesque fronde ancrée sur terre et se déployant dans l’espace sur plus de 70.000km. De quoi accrocher au câble une cabine et la faire monter dans l’espace !

Si ce concept est longtemps resté une utopie, notamment par l’impossibilité de réaliser un câble suffisamment résistant, l’apparition dans les années 2000 des nanotubes de carbone ont changé la donne. Comparé à l’acier, ce nouveau matériau a en effet, pour un poids égal, une résistance en gros 500 fois supérieure. La faisabilité d’un ascenseur reliant la terre à l’espace est dès lors redevenue envisageable (pour le futur…), à tel point qu’en 2018 l’entreprise japonaise Obayashi Corporation a envoyé en orbite un dispositif pour tester le concept.

Rappel sur la stabilité d’un corps en orbite circulaire

On a vu dans les billets précédents qu’un corps en orbite circulaire est stabilisé, dans son propre repère tournant, par deux forces qui s’opposent, la force centripète égale à l’attraction de la terre sur le corps, et la force centrifuge d’intensité  m.V²/R,  où :

m = masse du corps

V = vitesse du corps par rapport à un repère géocentrique

R = distance du corps au centre de la terre

Par commodité on va introduire la notion de vitesse angulaire ω, ou vitesse de rotation, exprimée par exemple en angle parcouru α par unité de temps. On sait que :

            V = \dfrac{dl}{dt}  , ω = \dfrac{d\alpha}{dt} , R = \dfrac{dl}{d\alpha} 

par conséquent V = ω . R

L’intensité de la force centrifuge peut donc s’écrire :  F = m . V² / R  = m . ω² . R .

La force centripète quant à elle est égale à  F = G . M . m / R²  où :

G = constante de gravitation universelle

M = masse de la terre

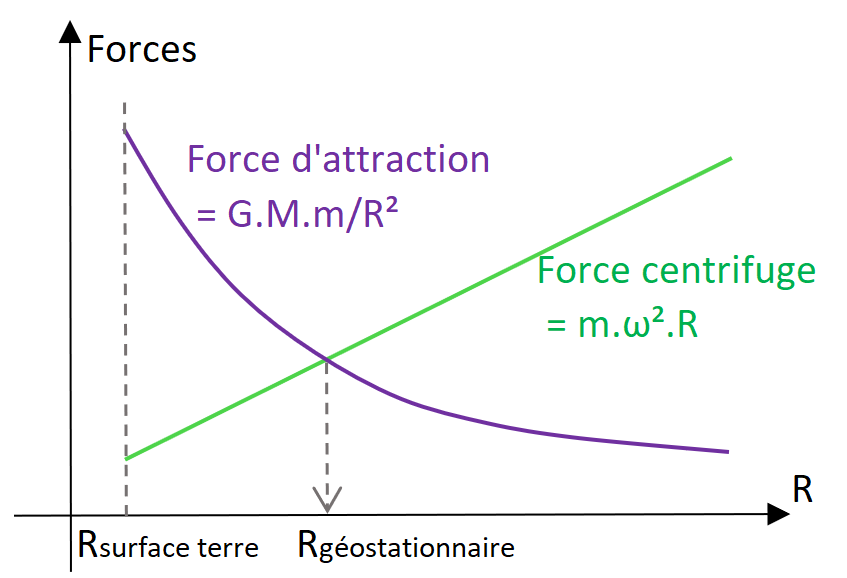
Les intensités de ces deux forces sont représentées sur le graphique ci-dessus. L’intersection des courbes correspond à l’altitude d’un corps géostationnaire comme on l’a vu dans le billet précédent, la force d’attraction terrestre étant exactement égale à la force centrifuge due à l’orbite circulaire du corps. En-dessous de ce point , la force d’attraction du corps est trop important par rapport à la force centrifuge et le corps va tomber. Au-dessus de ce point, la force d’attraction est trop faible pour retenir le corps à l’altitude considérée, et la force centrifuge va le faire s’élever.

Construire un ascenseur spatial

Depuis un satellite en orbite géostationnaire, à environ 36.000km d’altitude, imaginez que je déroule un gigantesque câble à la fois vers le bas et vers le haut.

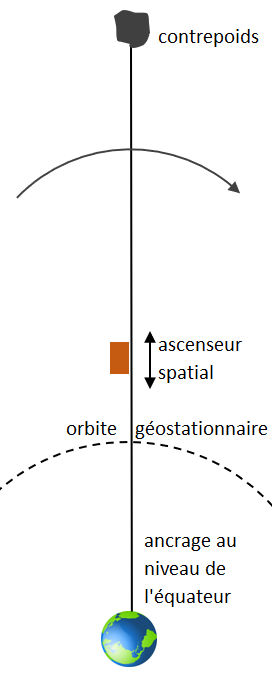
Vers le bas, l’attraction terrestre sur le câble est supérieure à la force centrifuge qui s’y applique, et le câble va se dérouler naturellement jusqu’à un point sur terre  correspondant à la verticale du satellite. Vers le haut, à l’inverse l’attraction terrestre est inférieure à la force centrifuge, et le câble monte de lui-même verticalement. On obtient alors un système équilibré, avec un câble d’environ 150.000km, longueur qu’on va en fait limiter à environ 100.000km en y ajoutant un contrepoids à l’extrémité haute.

Reste à imaginer un ascenseur qui monte le long du câble, et nous avons notre ascenseur spatial. En principe, car de très nombreuses difficultés devront d’abord être résolues : stabilité générale du système, percussion à très grande vitesse par des météorites ou des débris spatiaux, radiations, risques liés à la foudre … Et surtout capacité à fabriquer un tel câble.

La force de traction maximale dans le câble se situe au niveau de l’orbite géostationnaire, elle est due au poids propre du câble en-dessous de ce point. Au niveau du sol, cette force est nulle et permet d’accrocher  le câble sans effort. On va donc plutôt utiliser un câble de section croissante, maximum au niveau géostationnaire, minimum côté terre et côté espace. Ce câble prendrait la forme d’un mince ruban de nanotubes de carbone d’environ 1m de large, de section variable.

Verra-t-on dans quelques dizaines d’années cet ascenseur spatial ? D’ici là il reste un nombre incroyable de défis techniques à relever.

–oo—oo–