Le calcul infinitésimal est né au XVIIe siècle, avec les premières  formalisations de Newton et de Leibniz. Il comprend deux branches, le calcul différentiel (les dérivées) et le calcul intégral. Il s’agit d’outils essentiels, notamment en physique, comme on va le voir.

Pour faciliter la lecture, certaines hypothèses ont été retenues, la généralisation des démonstrations pouvant être faite sans difficultés : on est dans le domaine des nombres  réels et les fonctions sont continues, de signe constant.

Dérivées

Soit une fonction y=f(x). Au voisinage d’un point A d’abscisse x_0,  on cherche à savoir comment évolue la fonction f : dans quel sens, plus ou moins rapidement etc.

Considérons un autre point B, voisin de A, d’abscisse x = x_0+h.

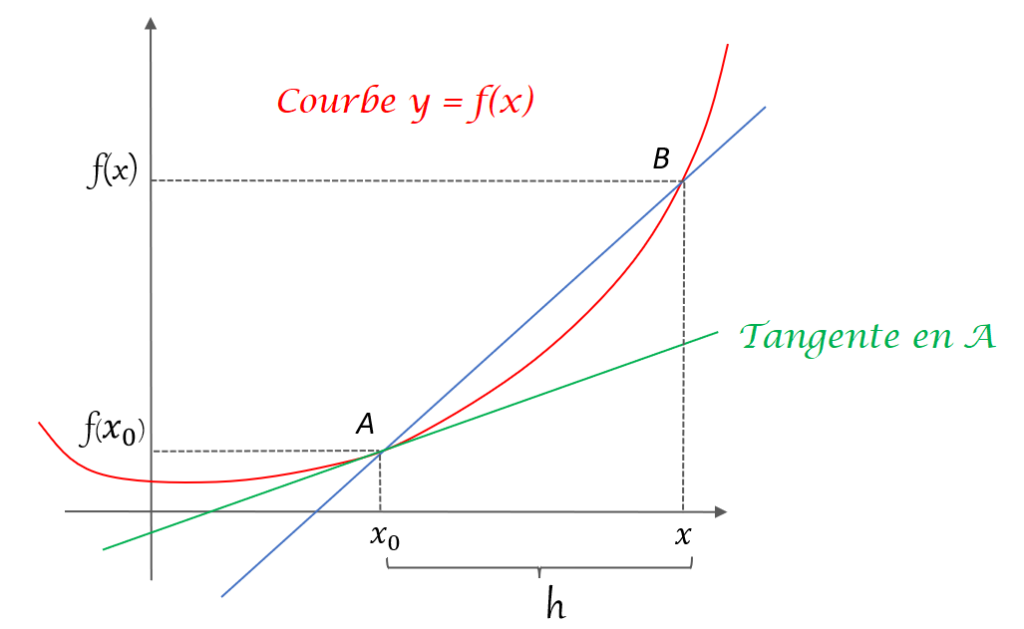
Le taux de croissance ou de décroissance de la droite AB, qu’on appelle aussi sa pente ou son coefficient directeur, est égal à :

 T_{AB}  = \dfrac{f(x)-f(x_0)}{x-x_0}

Lorsqu’on fait tendre h vers 0, soit B vers A,  la droite AB tend vers la tangente en A et le coefficient directeur T_{AB}  tend vers la pente de cette tangente. Cette limite est appelée dérivée de f en x_0  , notée f'(x_0) :

f'(x_0)=\lim_{x \to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}

Plus généralement la dérivée en tout point x de la fonction y = f(x) est notée f’(x).

Pour les physiciens, la notation traditionnelle est \dfrac{df}{dx} ou \dfrac{dy}{dx}, notation symbolique correspondant à la limite de \dfrac{\varDelta y}{\varDelta x} quand \varDelta x tend vers 0.

Utilisation des dérivées

Des tableaux mathématiques donnent les listes des dérivées d’un grand nombre de fonctions. Voyons un exemple simple avec la fonction f(x) = x² :

T_{AB}=\dfrac{f(x)-f(x_0)}{x-x_0}=\dfrac{(x_0+h)²-x_0²}{x-x_0}=\dfrac{(x_0²+2x_0h+h²)-x_0²}{h}=2x_0+h

La limite de  T_{AB} quand h tend vers 0 est 2x_0 . La dérivée de f(x) est donc f’(x)=2x.

Notons qu’on peut de la même manière dériver à nouveau la fonction f’(x) , ce qui donne dans notre exemple f ‘’(x) = 2.

En physique, la dérivée va servir par exemple à calculer la vitesse V d’un corps en mouvement. Prenons le cas simple d’une voiture qui roule en ligne droite, sa distance parcourue étant notée (L) qui varie en fonction du temps suivant une fonction  L = f(t).

La vitesse de la voiture au temps t_0 est le taux de croissance ΔL pendant un intervalle de temps Δt très petit au voisinage de t_0 , soit la limite de \dfrac{dL}{dt} quand dt tend vers 0, ce qui est la définition de la dérivée de f : V(t_0) = L’(t_0).

Quant à l’accélération (ou décélération) γ de la voiture au temps t_0, elle est de la même manière égale au taux de croissance (ou décroissance) de la vitesse pendant un intervalle de temps Δt très petit au voisinage de t_0, soit cette fois-ci  γ(t_0) = V’(t_0) = L’’(t_0) dérivée seconde de L(t) en t_0.

Intégrale

L’intégrale est en quelque sorte l’inverse de la dérivée. Définissons d’abord ce qu’on appelle les fonctions  primitives de f(x), l’inverse des dérivées justement :

F(x) est une primitive de f(x) si sa dérivée est égale à f(x) : F’(x) = f(x) .

Notons pour la suite que F(x) est une primitive à une constante près, puisque la dérivée d’une constante est nulle.

Définissons l’aire sous la courbe f(x) entre les abscisses 0 et x , hachurée en bleu sur le croquis, notée A(x). Cette aire A(x) est une fonction de x. Pour faciliter la démonstration, on choisit f(x) croissante, la démonstration se généralisant facilement.

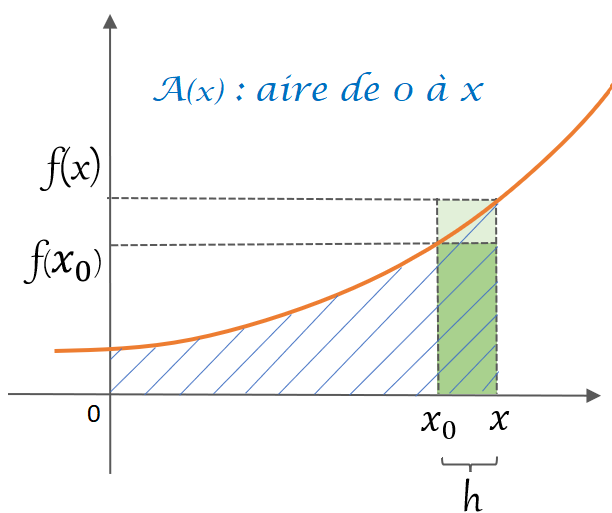
Considérons l’aire sous la courbe f(x) entre les abscisses x_o et x=x_0+h, égale à A(x)-A(x_0). Cette aire, limitée au-dessus par la courbe orange f(x),  est comprise entre les deux rectangles (en vert) de surfaces f(x_0).h et f(x).h :

f(x_0).h\leqslant A(x) - A(x_0) \leqslant f(x).h

soit

f(x_0)\leqslant\dfrac{A(x)-A(x_0)}{x-x_0}\leqslant f(x)

Quand h tend vers 0, soit x vers x_0, le terme central a pour limite comme on l’a vu la dérivée de A(x) et donc :

f(x_0) \leqslant  A’(x_0) \leqslant f (x_0)  

soit  A’(x_0) = f(x_0)

Par conséquent l’aire A(x) est une primitive de f(x), notée F(x).

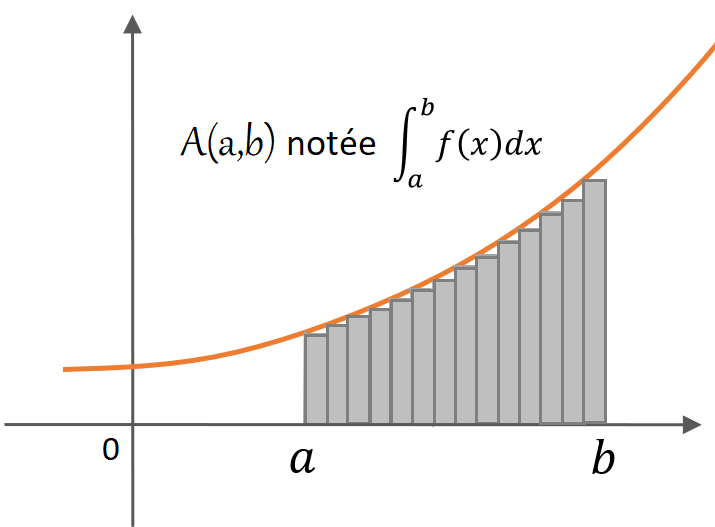
Plus généralement l’aire A(a,b) entre les points d’abscisse a et b sera appelée « intégrale de a à b  de f(x)dx », notée \int_{a}^b f\,(x)\,dx .

Elle est égale à A(b) – A(a), d’où le théorème fondamental de l’analyse qui lie l’aire avec les primitives :

A(a,b) = \int_{a}^b f\,(x)\,dx = F(b) – F(a)

La notation de l’intégrale représente en fait la somme des multiples rectangles découpant verticalement A(a,b) en tranches verticales de plus en plus fines quand leur largeur dx tend vers 0, comme le montre le croquis ci-contre.

Un exemple de calcul d’intégration figure dans le billet Aller dans l’espace – 3 Quitter la Terre .

On y trouve l’intégrale \int_{R}^\infty (1/D²).dD  où une primitive de 1/D² est -1/D d’où le résultat 1/R.

–oo—oo–