Fonction de 2 variables, dérivées partielles

Le billet  Calcul infinitésimal – Dérivées et intégrales  a abordé la notion de dérivée d’une fonction à une inconnue, y = f(x).

On a vu que f'(x_0), dérivée de f en x_0 , est la pente de la tangente en x_0 à la courbe y=f(x), soit tgα(x_0) . Cette dérivée est également notée par les physiciens \dfrac{dy}{dx}(x_0) , notation différentielle.

Or en physique beaucoup de fonctions dépendent non pas d’une mais de plusieurs inconnues.

Prenons par exemple le volume d’un cône de hauteur h et de rayon r à sa base, donné par la fonction de 2 variables  f(h,r) = π r² h/3  .

La variation de cette fonction f(h,r) par rapport à l’une seulement des variables, l’autre étant gardée constante, s’appelle dérivée partielle. On note \frac{\partial f}{\partial h} ou \frac{\partial f}{\partial r} les dérivées partielles de f par rapport à h ou à r.

De même on peut calculer les dérivées partielles secondes de f . En dérivant \frac{\partial f}{\partial h}  ou \frac{\partial f}{\partial r}  une nouvelle fois par rapport à h ou à r, l’autre variable étant à nouveau gardée constante, on obtient 4 résultats notés : \frac{\partial^2f}{\partial h^2} , \frac{\partial^2f}{\partial r \partial h} , \frac{\partial^2f}{\partial r^2} , \frac{\partial^2f}{\partial h \partial r} .

On démontre que pour les fonctions usuelles continues,  \frac{\partial^2f}{\partial r \partial h}=\frac{\partial^2f}{\partial h \partial r}  , l’ordre de dérivation est indifférent.

Calculons quelques dérivées partielles de notre fonction f(h,r) :

\frac{\partial f}{\partial r} = π . 2r . h/3  puis  \frac{\partial^2f}{\partial r^2}  = π . 2h/3    dérivée première puis seconde de f par rapport à r, h étant constante, ou encore   \frac{\partial^2f}{\partial r \partial h}=\frac{\partial^2f}{\partial h \partial r}  = 2πr/3 dérivées partielles secondes par rapport aux deux variables.

Équation de d’Alembert

Jean Le Rond d’Alembert est un esprit brillant du 18^e siècle, mathématicien, physicien et encyclopédiste. En 1747 il publie un mémoire « Recherches sur la courbe que forme une corde tendue, mise en vibration » qui sera une contribution majeure à la physique mathématique en utilisant une nouvelle approche, les dérivées partielles. Leur utilisation est à la base de la théorie de la propagation des ondes.

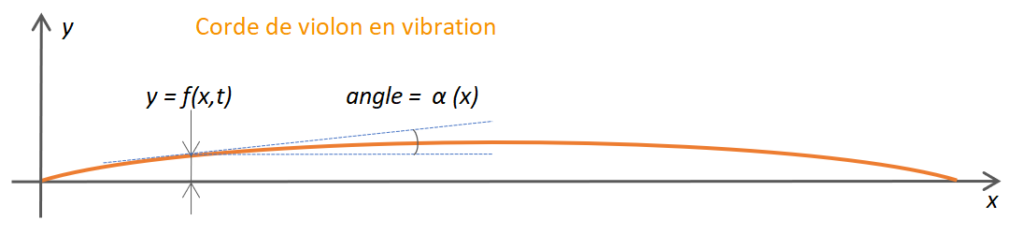
Considérons une corde de violon qui vibre, dont la forme est représentée par une fonction dépendant de 2 variables, l’abscisse x et le temps t. Plusieurs hypothèses simplificatrices sont choisies :

• la corde de masse linéaire μ est tendue par une force F, constante sur la longueur,
• un très petit brin de corde, situé entre les abscisses x et (x+dx), de longueur dx, a une masse μ.dx et un poids négligeable par rapport à F,
• l’amplitude de la vibration étant faible, l’angle α (x) est très petit, d’où les équivalences
  α \approx tg(α) \approx sin(α) (1) , la tangente à la courbe au point (x) étant égale à la dérivée de f en x, ici \frac{\partial y}{\partial x}.

D’après la loi fondamentale de la dynamique de Newton, la somme des forces qui s’appliquent sur le petit brin de corde est égale à sa masse multipliée par son accélération,  \sum\overrightarrow{F}=m . \overrightarrow\gamma , ce qui donne :

\overrightarrow{Tg}(x,t) +\overrightarrow{Td} (x+dx,t) = μ.dx. \overrightarrow\gamma (x,t)

On projette ces vecteurs sur l’axe des y :

F sin α(x+dx,t) - F sin α(x,t) = μ.dx.\frac{\partial^2 y}{\partial t^2}

avec            F . [α(x+dx,t) - α(x,t)] . \frac{1}{dx} = F . \frac{\partial\alpha}{dx}

et                \alpha\approx tg(α) =  \frac{\partial y}{dx}

ce qui nous donne in fine :         μ . \dfrac{\partial^2 y}{\partial t^2} = F. \dfrac{\partial^2 y}{\partial x^2}

Jean d’Alembert établit ainsi une équation différentielle fondamentale, aux dérivées partielles, qui décrit la variation dans le temps et dans l’espace d’une onde transversale. Il donne les solutions générales de cette équation, notamment de formes sinusoïdales.

Contribution majeure, l’équation d’onde de d’Alembert servira dans de nombreux phénomènes ondulatoires, mécaniques, électromagnétiques et lumineux.

–oo–oo–

1. Approximation de Gauss pour les petits angles. Prenons un petit angle α=1° par exemple :
   α =  π/180 radian = 0,017453
   sin α = 0,017452
   tg  α = 0,017455
   ces 3 valeurs ne divergeant qu’à la 6^e décimale, négligeable pour notre démonstration physique.