Le billet précédent nous a montré que deux évènements qui évoluent ensemble n’ont pas forcément de lien de causalité. Ils peuvent cependant être liés par une corrélation, c’est un cas  fréquent. Par exemple la vente de crèmes glacées et celle de lunettes de soleil sont corrélées. L’une n’est pas la cause de l’autre, mais elles évoluent pareillement car liées toutes les deux à la météo, leur causalité commune.

Deux séries de mesures (Xi) et (Yi) pour chacun de ces deux événements, dans notre exemple les chiffres d’affaires des ventes de glaces et de lunettes de soleil à diverses dates, sont liées par un lien statistique mesurable.

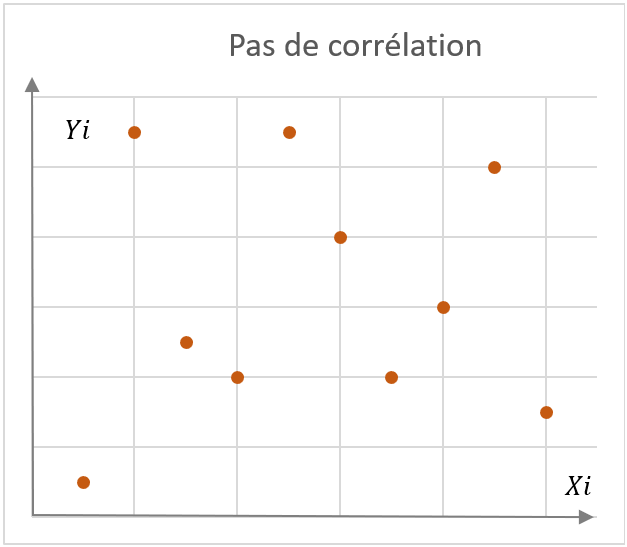
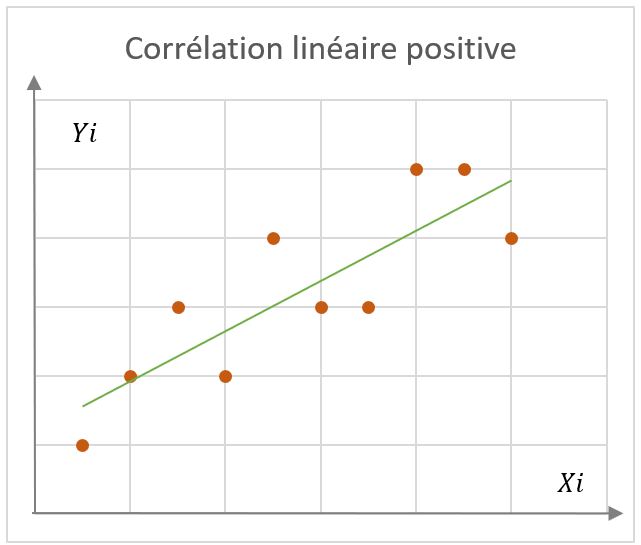
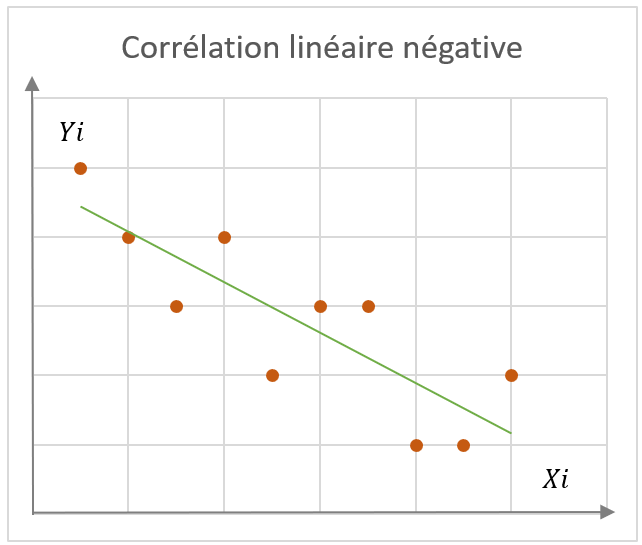
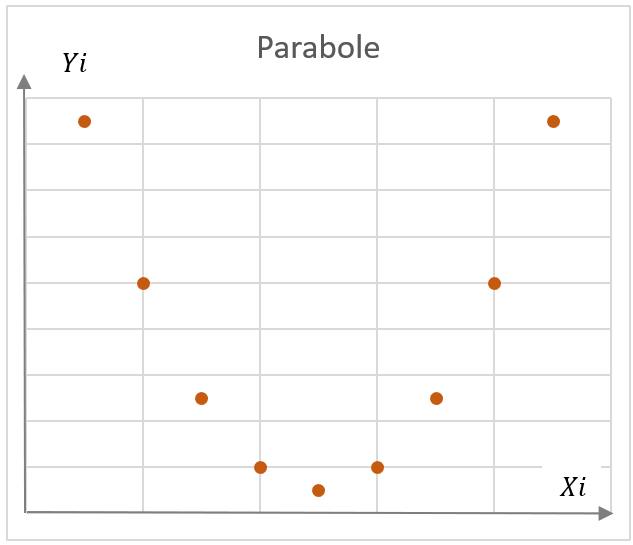
Pour y voir clair, on va tracer les couples (x_i,y_i) sur un graphique, et observer le nuage de points obtenu. Dans les exemples caractéristiques ci-contre, on distingue plusieurs schémas types :

• Un nuage sans corrélation visible
• Un nuage avec corrélation linéaire, positive ou négative
• Un nuage représentant une forme mathématique, ici par exemple une parabole.

Droite de régression

Arrêtons-nous sur la corrélation linéaire, la plus fréquente, qui se traduit par une droite d’équation y=f(x)=ax+b passant au plus près de l’ensemble des points. On parle de droite de régression, car on a simplifié la réalité d’un ensemble de données par une droite. Avec l’équation de la droite, on va aussi pouvoir, pour une nouvelle valeur , calculer une prévision de sa valeur corrélée .

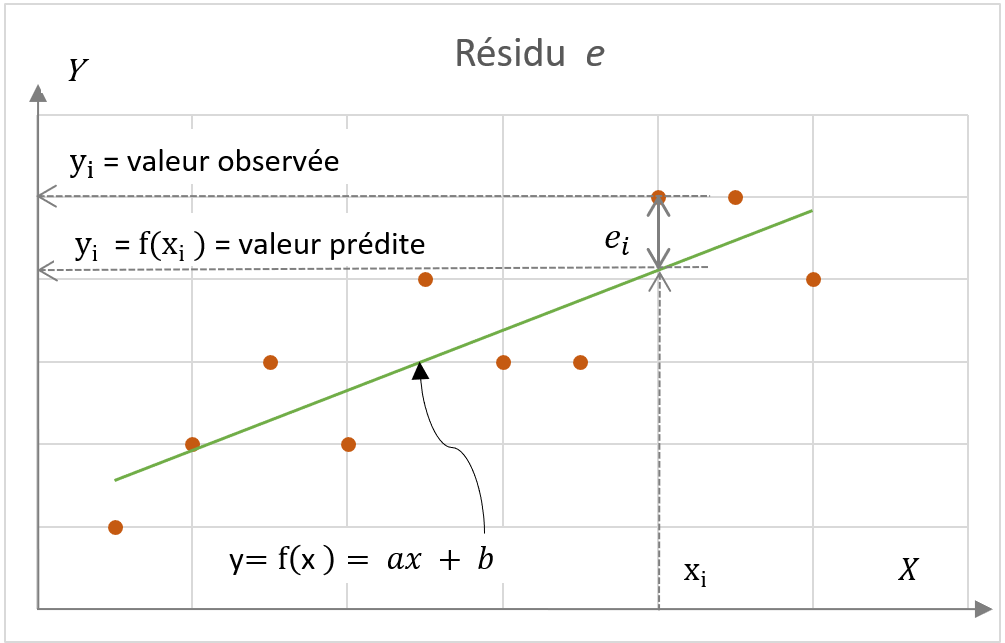
Si cette droite représente au mieux le nuage de points, le schéma ci-contre montre cependant que pour une donnée mesurée x_i, il y a une distance entre la donnée corrélée y_i et le point sur la droite f({x_i}), appelée résidu : e_i=y_i-f({x_i}).

Se pose alors la question suivante : y a-t-il une droite particulière qui traduit au mieux la corrélation, c’est-à-dire qui minimise les distances e_i  ?

Méthode des moindres carrés

On pourrait penser utiliser les  e_i (leurs valeurs absolues) et chercher à minimiser leur moyenne par exemple. Mais on montre mathématiquement que la droite ainsi obtenue n’est pas optimum.

Gauss et Legendre ont élaboré séparément au début du 19^e siècle un modèle appelé la « méthode des moindres carrés ». Il s’agit de chercher à minimiser la somme des carrés des e_i , les mathématiciens ayant démontré :

• que cette méthode permet de calculer les paramètres a et b de l’équation de la droite de régression (1),
• que cette droite est unique,
• et qu’elle donne bien la meilleure droite tant pour expliquer un évènement que pour le prédire.

Coefficient de corrélation de Pearson

Karl Pearson a élaboré ensuite son coefficient de corrélation r, qui évalue le degré de  dépendance entre les séries (Xi) et (Yi)  (1). Ce coefficient r est compris entre -1 et +1, le signe négatif ou positif traduisant le fait que les séries évoluent en sens contraire ou dans le même sens, et les valeurs -1 et +1 traduisant une corrélation totale.

Plus r est proche de +1, ou de -1, plus la droite de régression est ajustée. Pour fixer les idées:

Corrélation positive	Corrélation négative	Degré de corrélation r
0,0 à 0,1	0,0 à -0,1	Pas de corrélation
0,1 à 0,3	-0,1 à -0,3	Corrélation faible
0,3 à 0,5	-0,3 à -0,5	Corrélation moyenne
0,5 à 0,7	-0,5 à -0,7	Corrélation élevée
0,7 à 1,0	-0,7 à -1,0	Corrélation très élevée

Si ce coefficient de corrélation r est très utile pour mesurer la force d’une corrélation, son interprétation est délicate, et d’autres approches sont possibles.

Venons-en aux travaux pratiques

Les graphiques qui suivent sont tracés à l’aide du logiciel Excel, qui non seulement permet de tracer automatiquement la droite de régression, mais aussi donne son équation et calcule le coefficient de corrélation de Pearson r, évitant ainsi des calculs fastidieux !

Un premier graphique “pas de corrélation”, figurant au début de ce billet, représente des données (Xi) et (Yi) prises au hasard. Leur coefficient de Pearson r est de 0,067 montrant bien cette absence de corrélation.

Un autre exemple plus réel : la corrélation entre les émissions de CO2 dans le monde et l’évolution de la température moyenne mondiale entre 2000 à 2019. Le coefficient r = 0,98 montre une forte corrélation entre CO2 et température.

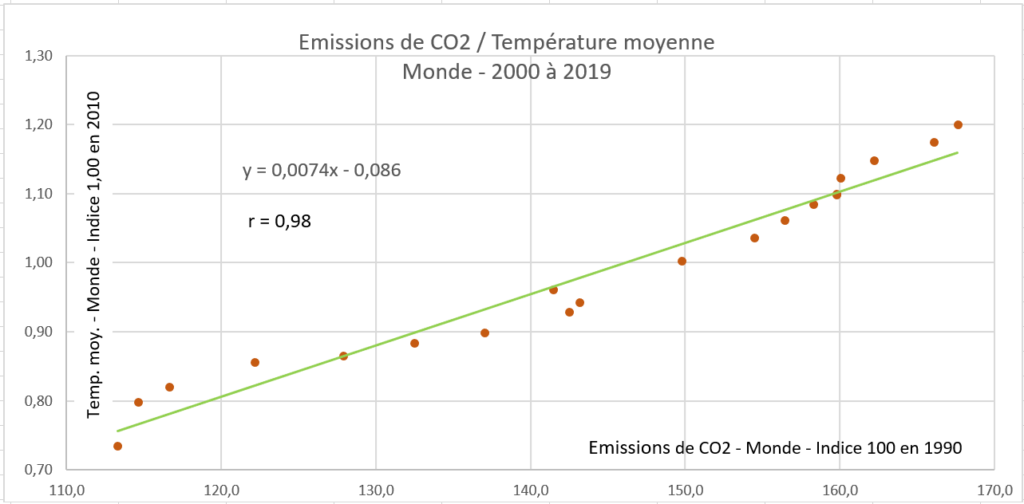
En conclusion, l’étude d’une corrélation à l’aide des outils développés ci-avant est très utile pour comprendre un phénomène. On les utilisent dans de nombreux domaines : finance, sociologie, biologie, anthropométrie etc.

Mais n’oublions pas qu’une corrélation , même totale, n’est pas forcément une causalité.

—oo—oo—

Les formules sont compliquées ; les voici pour être complet:

1. a = \frac{\sigma_{xy}}{\sigma_x^2} et b = \overline{y} - a.\overline{x}
2. r = \frac{\sigma_{xy}}{\sigma_x . \sigma_y}
   où
   \overline{x} et \overline{y} sont les moyennes des x_i et des y_i
   \sigma_{xy} = \frac{1}{n}\sum (x_i-\overline{x}) (y_i-\overline{y}) , \sigma_x^2=\frac{1}{n}\sum(x_i-\overline{x})^2 et \sigma_y^2=\frac{1}{n}\sum(y_i-\overline{y})^2