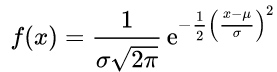On s’est longtemps demandé si le hasard suivait une loi.

En répétant un grand nombre de fois une épreuve aléatoire, par exemple le lancer d’une pièce à pile ou face, va-t-on constater que la dispersion des résultats suit une loi particulière ?

Une épreuve répétée

Une même épreuve peut être répétée autant de fois qu’on le souhaite : lancer de dés, tirage de boules de loto, jeu de la roulette… Restons sur le lancer d’une pièce bien équilibrée, qui a une chance sur deux de tomber sur pile ou sur face, et considérons une succession de 10 lancers par exemple.

On peut écrire le résultat de ces lancers sous la forme d’une série : par exemple PPFFPFPFFF, où Pile figure 4 fois et Face 6 fois.

Si on écrit toutes les séries possibles, il y a bien sur 2 possibilités 10 fois de suite, soit 2^{10} ou 1.024 solutions, chacune étant équiprobable.

On apprend en mathématiques que, parmi ces 1.024 séries possibles, correspondant à n = 10 lancers, le nombre d’entre elles comprenant k fois Pile (ou Face) est donné par la « combinaison » :

\binom{n}{k}=\frac{n!}{k! (n-k)!}

Par exemple avec k = 4 fois Pile :

\binom{10}{4}=\frac{10!}{4! (10-4)!}=\frac{(10.9.8.7.6.5.4.3.2.1)}{(4.3.2.1) (6.5.4.3.2.1)}=210 fois

La probabilité d’obtenir k fois Pile est de \binom{n}{k} divisé par 2^{n} , dans notre exemple 210 / 1024 = 20,5% , et peut se traduire par un histogramme en fonction de k :

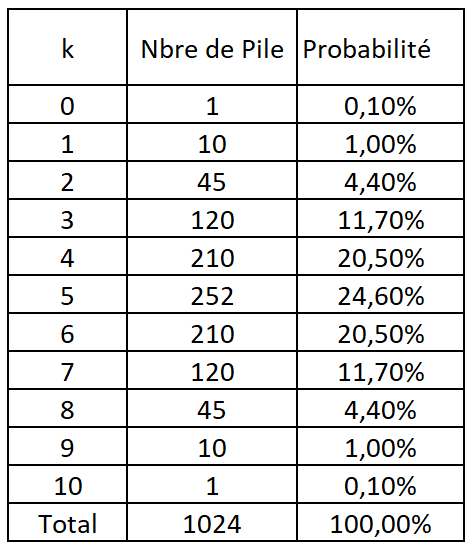
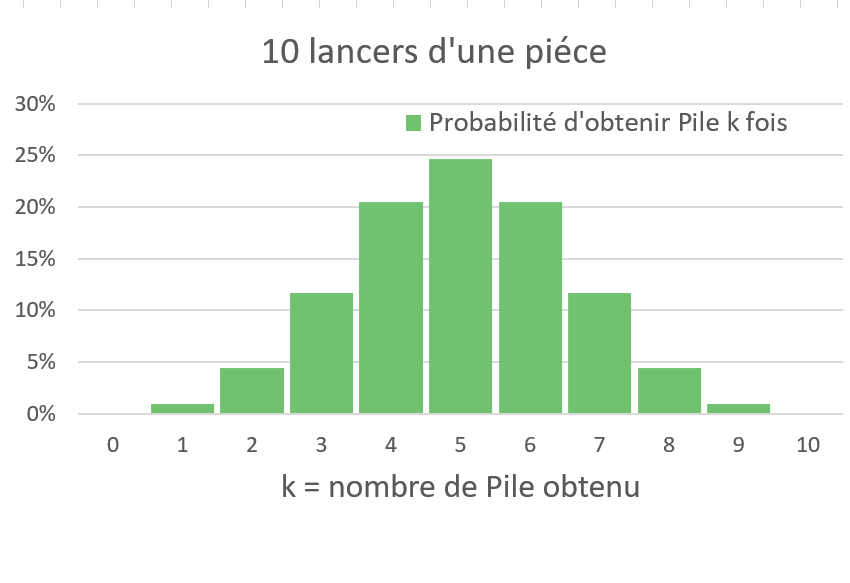
On comprend bien que les barres centrales sont plus grandes que les barres des extrêmes parce qu’il y a moins de solutions pour une pièce de tomber presque toujours sur pile ou presque toujours sur face. Il suffit d’écrire toutes les solutions possibles et de les compter pour s’en convaincre. On sait également que la somme des probabilités est égale à 100%.

Planche de Galton

Sir Francis Galton illustra cet histogramme avec sa « planche » qu’on voit dans la vidéo qui suit.

Une bille peut descendre successivement soit à gauche G soit à droite D. Elle décrit donc une série par exemple du type GGDDGDGDDD, le total des G (ou des D) étant équivalent au nombre k vu plus haut avec les lancers de pièce. On retrouve la même forme d’histogramme.

Répétons l’épreuve un grand nombre de fois

Revenons à notre pile ou face. Plus le nombre de lancers devient grand, plus on constate que l’histogramme tend à prendre la forme d’une courbe en cloche. Par exemple ici avec 60 lancers, on voit la courbe se dessiner :

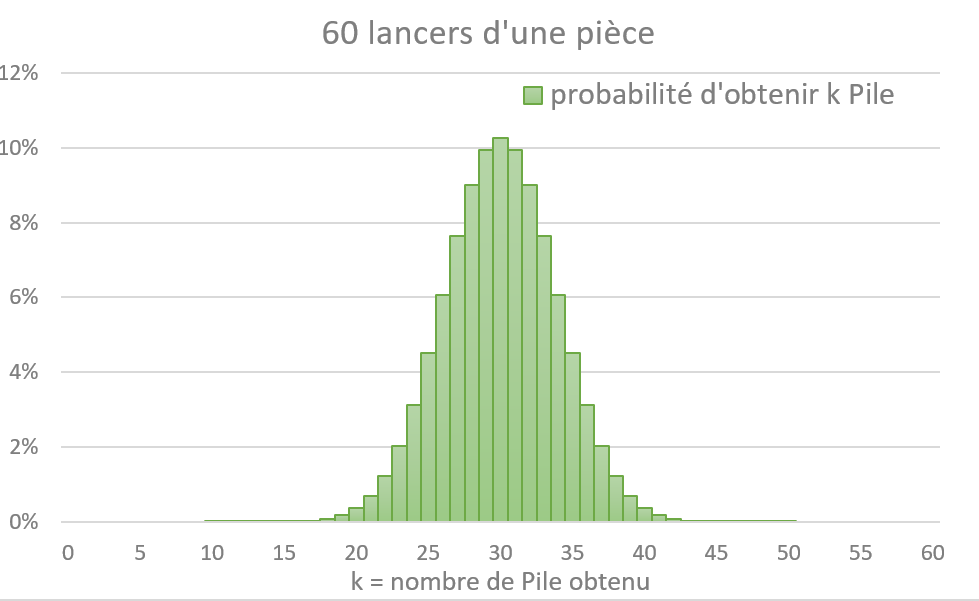
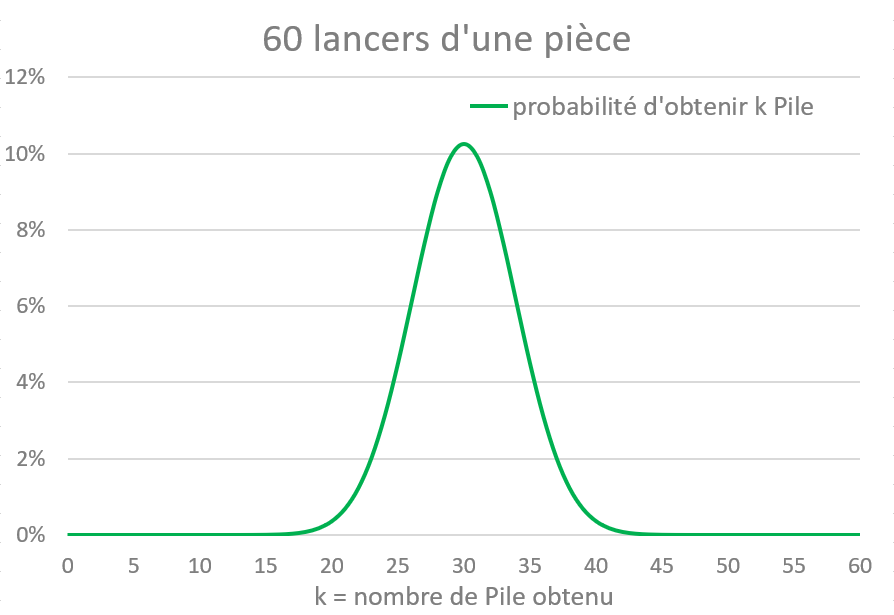
Dans la vie quotidienne, on a constaté que beaucoup de phénomènes, résultants de l’addition de multiples petites causes indépendantes et aléatoires, se traduisent par une courbe en cloche similaire : répartition de la taille d’un grand nombre de personnes, des  poids d’articles identiques, de données météorologiques … Comme pour le jeu de pile ou face, les phénomènes évoqués résultent de nombreux petits hasards successifs, dont l’addition répond aux probabilités décrites ci-dessus, la courbe de ces probabilités étant d’autant plus régulière que le nombre d’épreuves est grand.

Au 18e siècle, les mathématiciens de Moivre et Laplace ont établi que cette courbe en cloche représente une fonction précise, assez complexe , appelée loi normale (1).

Ainsi un grand nombre de phénomènes naturels (médecine, sciences sociales, physique, finances…) obéissent à cette loi normale, malgré les multiples causes aléatoires inconnues dont ils sont l’objet. La courbe de Gauss est ainsi remarquable par son universalité.

Dans le billet qui suit, on va en dire un peu plus sur cette loi normale.

–oo—oo–