Le billet précédent souligne que beaucoup de phénomènes résultants de l’addition de multiples petites causes indépendantes et aléatoires, suivent la « loi normale », traduite par une fonction spécifique (1) et représentée par une courbe en cloche de caractéristiques bien définies.

Quelles sont ces caractéristiques? Partons d’un exemple qui nous aidera à mieux comprendre.

La taille de 5.000 femmes

Le grand magasin néerlandais De Bijenkorf a procédé en 1947 à une campagne exhaustive de mensurations auprès de 5.000 femmes (2). Cette série de 5.000 tailles a permis de tracer un histogramme, avec lequel on voit apparaître une courbe en cloche caractéristique de la loi normale. Bien sûr, comme pour la planche de Galton dont on a parlé dans le billet précédent, l’exactitude n’est pas parfaite, mais suffisamment proche.

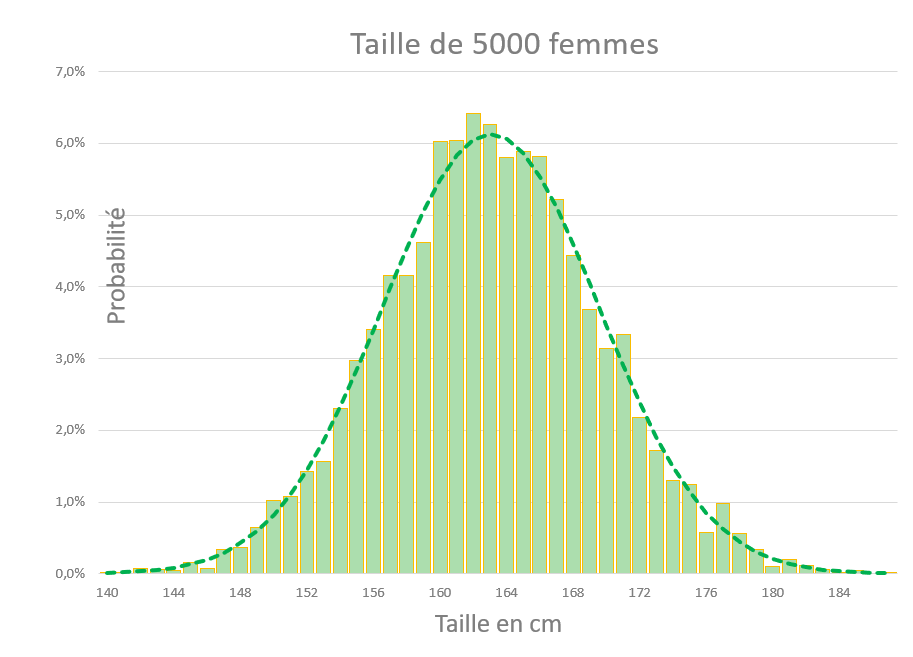
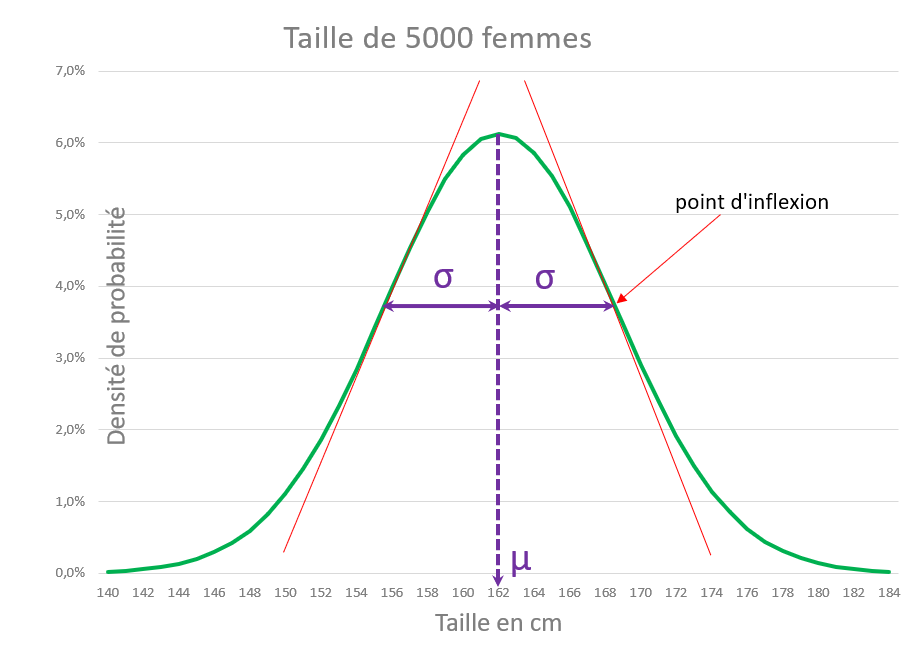
La courbe a un sommet d’abscisse μ correspondant approximativement à la moyenne des 5.000 mesures, dans notre cas 162cm. C’est la taille la plus probable de la série.

La courbe est symétrique, ce qui veut dire qu’il y a autant de tailles supérieures à 162cm, que de tailles inférieures. Elle a aussi deux points d’inflexion (3), qui déterminent en quelque sorte la « largeur » de la cloche, c’est-à-dire la plus ou moins grand dispersion des mesures. On appelle « écart-type » noté σ cette donnée, égal à 6,5 cm dans notre cas.

En résumé, la fonction (1) et sa courbe en cloche ont deux seules caractéristiques notées μ et σ, qui les  déterminent complétement.

Densité de probabilité

La probabilité pour que la taille x soit égale à une valeur donnée, 160cm par exemple, a un sens dans le cas d’un histogramme. Elle correspond à la barre de hauteur 6% et de largeur 1 cm, se rappelant que la somme de toutes les barres correspond à une aire totale de 100% ou 1. Il s’agit en fait de la probabilité pour qu’une femme ait une taille comprise entre 159,5cm et 160,5cm.

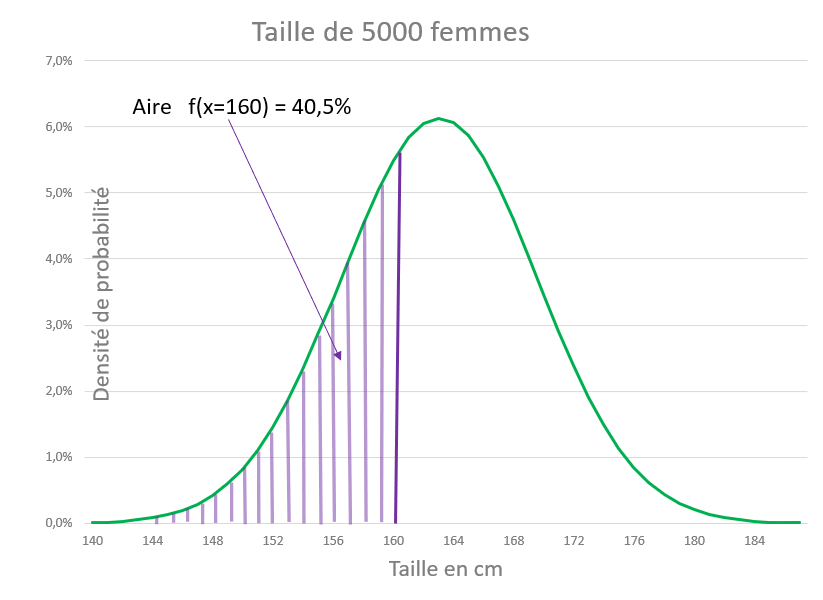
Cependant sur la courbe de Gauss, la probabilité pour qu’une femme mesure très exactement 160cm, avec une précision infinie, n’a pas de sens. La fonction f(x) (1) représente en fait une « densité de probabilité », f(x=160) étant égal à la somme de toutes les probabilités correspondant à x \leqslant 160 c’est-à-dire à l’aire sous-tendue par la courbe jusque x = 160, dans notre exemple 40,5%.

On retrouvera notre barre d’histogramme comme suit : f (x=160,5) – f (x = 159,5) = 6%.

D’une façon générale, les courbes de Gauss définissent précisément les densités de probabilité associés à la fonction (1). On les calcule dans des tables spécifiques, ou plus facilement avec un tableur comme Excel.

Ecart-type

Considérons cette fois 3 séries de données aboutissant à la même moyenne μ = 5 par exemple, mais dont les résultats sont plus ou moins dispersés autour de cette moyenne. Les écarts-types sont différents, d’autant plus grands que la dispersion est importante. Comme les aires sous les courbes sont toujours égales à 1, plus σ est grand et plus le sommet baisse.

Si on peut approximativement mesurer l’écart-type σ entre les points d’inflexion d’une courbe de Gauss, on peut en réalité le calculer facilement. On démontre en effet mathématiquement qu’avec une série de n variables (x_1, x_2, x_3, ...x_i,...x_n)   de moyenne \={x}, par exemple celle des tailles des femmes citée plus haut, l’écart-type se calcule à l’aide des formules suivantes :

Variance = V =  \dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_i -\={x})^2
Ecart-type = σ = \sqrt{V}

Dans notre exemple ce calcul donne 6,5cm.

L’utilisation de l’écart-type donne des probabilités très utiles dans de multiples cas, comme le montre le schéma ci-contre.

Au-delà de \pm 2σ , la probabilité d’existence est de moins de 5% . Dans l’exemple des tailles des femmes, 95% environ d’entre elles se situent dans la fourchette [(162- 2×6,5), (162+2×6,5)] soit
[149cm, 175cm]. Au-delà de \pm 3σ, la probabilité d’existence est quasi-nulle.

–oo–oo–

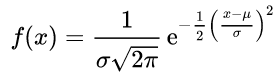
2. document web :  ces-stexupery.be/institue-sainte-marie/…/vandenbruaenne-andre

3. point d’inflexion : là où la tangente traverse la courbe