Une équation différentielle, un nom super tentant quand on est jeune et qu’on s’intéresse aux sciences. Je me souviens encore de ma première équation différentielle !
Mais qu’est-ce que c’est et à quoi ça peut bien servir ?

En voilà une belle illustration : le refroidissement d’un objet, un bloc de matière chauffé qui se refroidit à l’air libre par exemple. Comment s’évacue la chaleur du corps, à quelle vitesse ?
Il y a quelques siècles, le grand scientifique Newton énonça que le refroidissement d’un corps (sa baisse de température) était proportionnel à la différence de température entre ce corps et le milieu environnant. Loi qui paraît intuitivement logique, plus le corps est chaud plus il se refroidit rapidement et inversement.
La température du corps à l’instant t est notée T(t). On cherche donc à modéliser l’évolution de la fonction T(t) en fonction du temps.
Essayons de voir ce qui se passe entre deux instants proches t et t+dt, espacé d’un petit intervalle de temps dt.
La température du corps entre les instants t et t+dt va passer de T(t) à T(t+dt), avec une petite baisse de température dT= T(t+dt) – T(t).
D’après Newton donc, la baisse de température dT est proportionnelle à T(t), et bien sûr proportionnelle au temps passé dt.
On a donc dT = k . T(t) . dt
Où k étant une constante qui dépend du corps, de sa forme, de sa capacité plus ou moins grande à se refroidir rapidement etc.
Soit dT/dt = k . T(t) qu’on écrit aussi T’(t) = k . T(t)
puisqu’on reconnait en dT/dt la dérivée de T(t) par rapport au temps, c’est-à-dire la vitesse de refroidissement: voir le billet Calcul Infinitésimal – Dérivées et intégrales.
La température du corps T(t) et sa dérivée T’(t) sont donc proportionnelles , et voilà notre équation différentielle, certes très simple, c’est-à-dire une équation qui lie une fonction et sa dérivée.
On peut la résoudre facilement car on sait que la dérivée d’une fonction exponentielle et cette même fonction sont égales,
(e^t)' = e^t
et que : (e^{kt})' = k . e^{kt}
d’où la solution : T(t) = Ta . e^{kt}
où Ta est la température ambiante.
On peut vérifier qu’en dérivant T(t) = Ta . e^{kt}
On obtient bien : T’(t) = Ta . (e^{kt})' = Ta . k . e^{kt} = k. T(t)
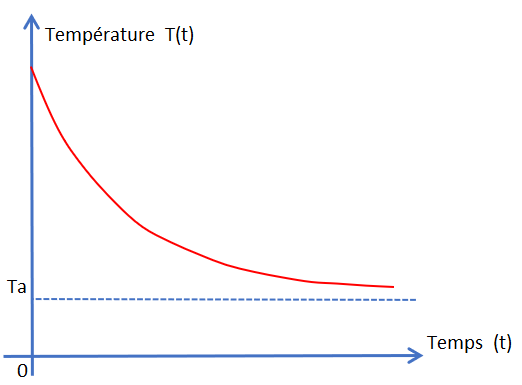
Voici la courbe de refroidissement. Celui-ci ralentit bien au fur et à mesure que la température du corps baisse.
Un grand nombre de phénomènes en physique sont régis par des équations différentielles. Les dérivées premières traduisent la vitesse de ces phénomènes, les dérivées secondes leur accélération.
–oo–oo–