Les notes naturelles
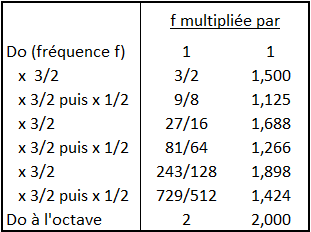
Partons d’une note quelconque, par exemple un do de fréquence f. Une octave au-dessus, on aura un do équivalent de fréquence 2f. Dans cet intervalle d’une octave, on va chercher à construire harmonieusement une gamme de notes.
Dans le billet précédent, on a vu qu’en multipliant la fréquence f par 3/2 c’était bien le cas. En progressant ainsi de quinte en quinte, on doit obtenir une série de notes consonantes entre elles. A noter que dès que la fréquence calculée sort de notre intervalle f / 2f , on la divise par 2, ce qui nous donne une note équivalente.
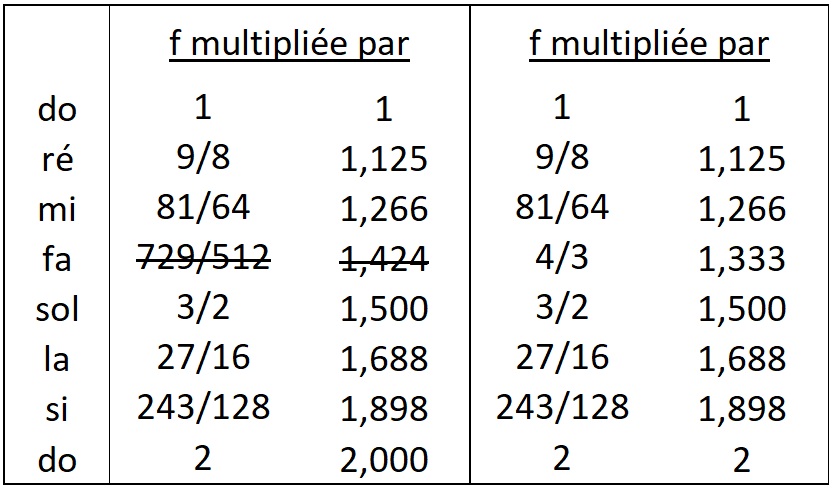
Mettons maintenant les 6 fréquences calculées dans un ordre croissant. On obtient alors la gamme connue de tous (do, ré, mi, fa, sol, la, si, do), à ceci près que :
- la dernière quinte aurait normalement une fréquence de (729/512) x (3/2) = 2187 / 1024 = 2,136 différente de 2,000 , cette fausse quinte étant problématique.
- pour le fa, on a préféré calculer une quinte à l’envers, une quarte, c’est-à-dire la note dont la quinte est le do à l’octave:
2 x \frac{1}{3/2} = 4/3 fraction plus simple que la fraction 729/512
Le fa d’origine est en réalité un fa#, que l’on retrouvera un peu plus loin.
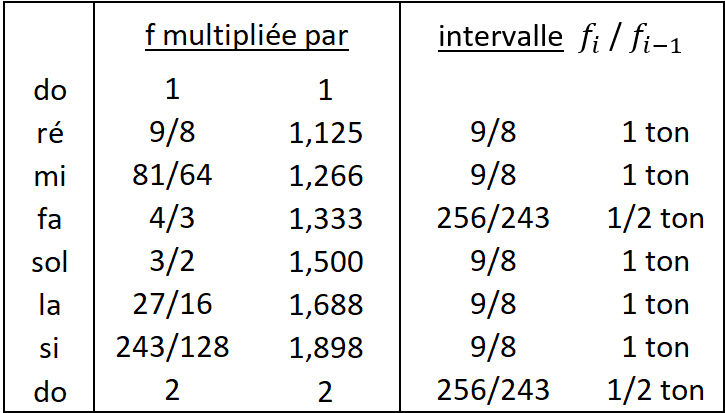
Les espaces obtenus entre les notes font apparaître 2 intervalles différents, appelés ton et demi-ton. La gamme classique comporte donc 7 notes irrégulièrement espacées.
Cette irrégularité conduit à une difficulté, l’impossibilité de transposer une musique (sauf à l’octave), c’est-à-dire de la jouer en montant ou en descendant d’un même nombre de notes. En décalant un chant de 2 notes vers le haut par exemple, pour éviter de chanter trop bas, on décale le chant de 1 ton 1/2 ou 2 tons selon les notes, ce qui modifie la ligne mélodique.
Pour surmonter cette difficulté, tout en créant plus de notes afin d’enrichir les mélodies, poursuivons le cycle des quintes.
La gamme chromatique
Une fois 12 cycles des quintes calculés, et les fréquences mises dans un ordre croissant, on obtient cette fois-ci la gamme chromatique ascendante complète, les nouvelles notes obtenues entre les 7 notes principales s’écrivant avec un #.
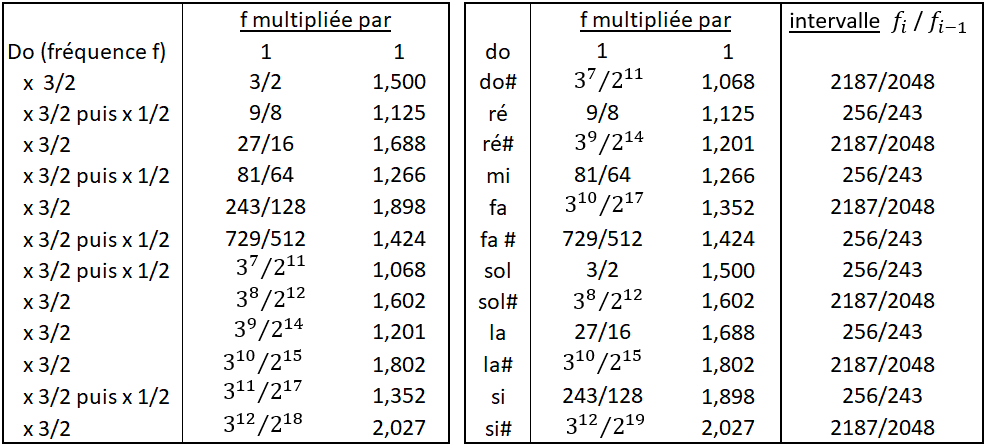
Deux constatations s’imposent:
- au bout de 12 cycles ascendants, on retombe pratiquement sur la fréquence recherchée 2,000f , plus précisément 2,027f correspondant à si#. Plutôt que de continuer le cycle des quintes, on va négliger l’écart, confondre le si# et le do et se contenter des 12 notes ainsi obtenues (1). Cet intervalle entre si# et do est appelé le comma pythagoricien. Il est précisément égal à 3^{12}/ 2^{19} soit environ 1,01364.
- les intervalles f_i/f_{(i-1)} qui se succèdent sont tous égaux à l’un des deux demi-ton différents mais proches, 256/243 ou 2187/2048, l’un étant un peu plus large que l’autre (2).
Notons au passage qu’on a retrouvé le fa# abandonné un peu avant, de fréquence 729/512.
Pour être complet, on peut aussi calculer le cycle des quintes cette fois-ci vers le bas, c’est-à-dire en divisant une fréquence de base par 1,5 à partir de notre do (c’est-à-dire en la multipliant par 2/3), toujours en replaçant la fréquence obtenue dans l’intervalle f / 2f :
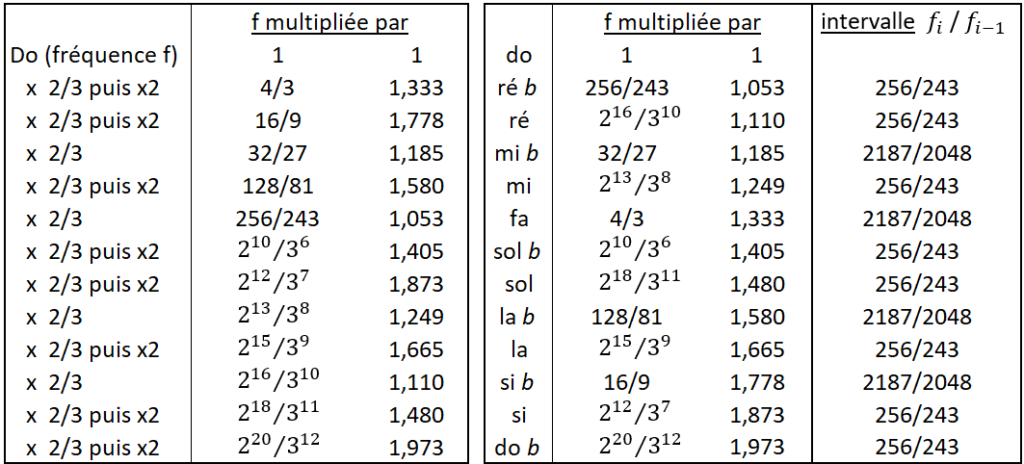
Au bout de 12 cycles descendants, on fait les mêmes constatations que précédemment, en retombant pratiquement sur la fréquence recherchée 2,000f , plus précisément 1,973f.
Mettons les 12 fréquences obtenues dans l’ordre, on obtient la gamme chromatique cette fois-ci descendante, les nouvelles notes obtenues entre les 7 notes principales s’écrivant avec un bémol. Les intervalles f_i/f_{(i-1)} qui se succèdent sont les mêmes 2 sortes de demi-tons, 256/243 ou 2187/2048 (2).
Les musiciens considèreront que 12 notes séparées d’un demi-ton sont suffisantes pour composer, et retiendront in fine les 8 premiers cycles ascendants plus les 3 premiers cycles descendants, ce qui donnera la gamme de Pythagore qui sera utilisée jusqu’au 17e siècle:
do – do# – ré – mi b – mi – fa – fa# – sol – sol# – la – si b – si – do
Difficultés concernant la gamme de Pythagore
La première d’entre elles résulte de la 12e quinte qui ne tombe pas pile sur une octave (1). Cette quinte naturelle va légèrement au-delà de l’octave, la dépassant d’un comma.
En ramenant cette douzième note à une octave, on obtient une quinte un peu courte, appelée quinte du loup en raison de sa dissonance. Les douze notes de la gamme de Pythagore correspondent donc à 11 quintes justes et une quinte fausse. Durant ces derniers siècles, de multiples recherches ont tenté soit d’éviter d’utiliser cette quinte, soit de répartir le comma en excès de différentes façons, créant ainsi autant de gammes différentes.
La deuxième difficulté résulte de l’impossibilité de transposer une mélodie de façon parfaite, puisqu’il y a deux demi-tons différents irrégulièrement espacés.
La gamme tempérée
Parmi les multiples solutions recherchées pour résoudre ces difficultés, l’une d’elles s’est imposée au 19e siècle, ajuster les 12 demi-tons entre les notes en 12 intervalles égaux.
Si on appelle r cet intervalle, on a la relation r^{12}= 2 puisqu’une octave comprend douze intervalles. Ce qui nous donne: r = 2^{1/12}\approx 1,0595 , au lieu de respectivement 1,0535 et 1,0679 pour les deux demi-tons Phytagoricien (2).

Il n’y a plus maintenant de quinte du loup, ni deux sortes de demi-ton, mais plus aucun intervalle n’est parfaitement juste. C’est une concession universelle que les musiciens accepteront tant elle se révèle efficace, facilitant la transposition dans n’importe quelle tonalité, et permettant à un grand nombre de musiciens de jouer ensemble.
L’accordage du piano se fait avec la gamme tempérée.
–oo–oo–
- Le cycle des quintes se reboucle « presque » avec un cycle d’octaves, mais pas parfaitement. En effet l’intervalle d’une succession de n quintes s’obtient en multipliant la fréquence de la note de base f par (3/2)^n , alors que pour un cycle de p octaves, f doit être multipliée par 2^p .
Il faudrait donc qu’on ait (3/2)^n = 2^p , ce qui revient à 3^n=2^{(n+p)}.
Comme une puissance de 3 ne peut pas être égale à une puissance de 2, c’est impossible. Cependant on constate que pour n = 12 et p = 7 , donc pour 12 quintes et 7 octaves, on a (3/2)^{12} = 129,746 et 2^7 = 128 , deux valeurs suffisamment proches pour qu’on décide de les confondre. - Il s’agit du 1/2 ton chromatique (2187/2048 \approx 1,0679) par exemple do – do# , et du 1/2 ton diatonique (256/243 \approx 1,0535) par exemple do# – ré.
Ces deux demi-tons successifs forme un ton : (2187/2048) x (256/243) = 1,125 .
Ils sont séparés par un comma: (2187/2048) / (256/243) \approx 1,01364 .