En 1733 Buffon, un grand scientifique naturaliste français, propose le problème amusant suivant.

Sur un parquet dont les lames ont une largeur L, on lance une aiguille de même longueur L . Quelle est la probabilité pour que l’aiguille coupe une rainure ?

J’ai croisé ce problème très jeune, au cours d’une visite du Palais de la découverte à Paris. Dans une des salles se trouvait une machine constituée de lames de parquets métalliques. En appuyant sur un bouton on lançait une aiguille en l’air. Un fois retombée, si et seulement si elle touchait 2 lames adjacentes, en coupant donc une rainure, un compteur marquait un point de plus. La machine affichait le rapport de ces points ramenés au nombre de lancés N, donc la probabilité recherchée.

Suivait la solution mathématique dont l’élégance, pourtant difficilement imaginable pour moi,  m’avait enthousiasmé ! La voici.

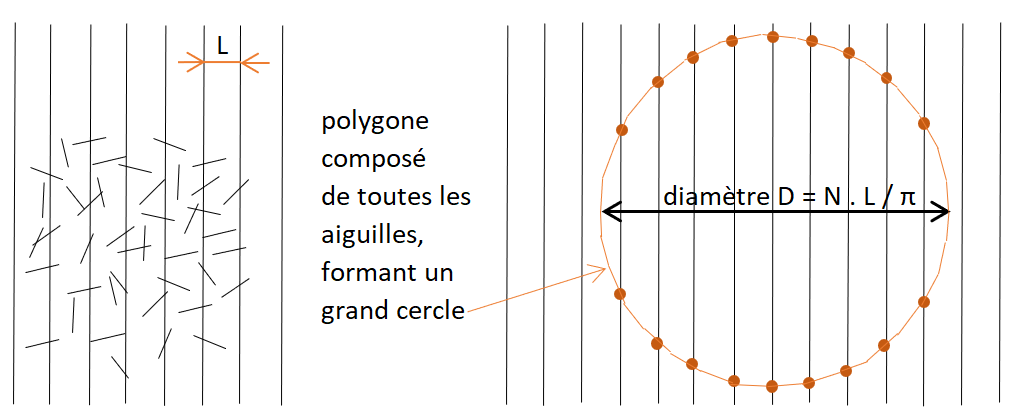
Supposons qu’on lance un grand nombre de fois (N) l’aiguille, qui tombe avec toutes les positions possibles, toutes avec la même probabilité. En mettant bout à bout toutes ces positions pour former un grand polygone régulier, on voit que si N devient très grand, le polygone tend vers un grand cercle.

Ce cercle a un périmètre P = N . L ,  et puisque vous connaissez la formule  P = π . D , on a alors   D = N . L / π   .

De part et d’autre de ce diamètre se situent deux demi-cercles qui coupent des rainures. En divisant le diamètre D par L , on obtient le nombre de fois où un demi-cercle coupe une rainure, soit  N/π . Et donc pour le cercle entier :  2N / π.

Si N lancés d’aiguille conduisent à  2N / π   intersections de rainures, pour chaque lancé d’aiguille, la probabilité de couper une rainure est égale à :   

2 / π

Mais que vient faire le nombre π dans cette affaire, on se le demande !

En tout cas, le compteur de la machine du Palais de la découverte tendait bien vers le bon résultat.