A la suite du billet précèdent, deux questions sont apparues :

• A quoi sont dues l’augmentation de l’entropie et la non réversibilité des phénomènes constatés ?
• A quoi correspond cette entropie ?

Pour comprendre ces notions, nous allons devoir descendre profondément dans la matière.

Les atomes constitutifs de la matière sont soit liés les uns aux autres, cas d’un solide, soit glissants les uns sur les autres, cas d’un liquide, soit pour le gaz séparés les uns des autres et agités en tous sens dans leur contenant. Dans tous les cas ils vibrent ou se déplacent dans l’espace, animés constamment d’une énergie interne. C’est cette énergie interne qu’on ressent sous forme de chaleur ; plus les atomes sont agités, plus c’est chaud. Si plus rien ne vibrait, si les atomes étaient immobiles, c’est qu’on aurait atteint la température du zéro absolu, 0°Kelvin ou -273°Celsius.

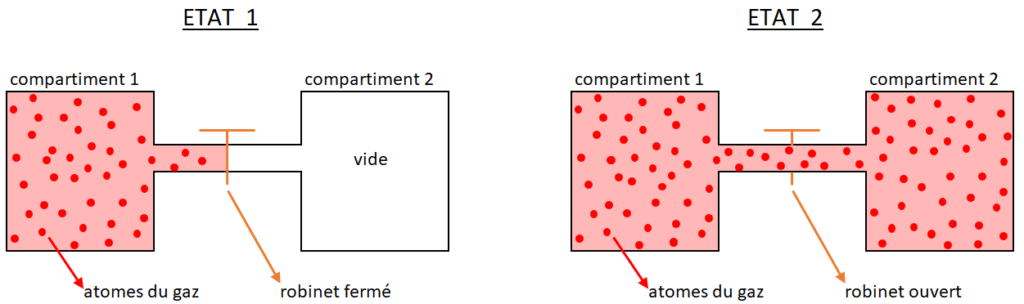
Regardons maintenant l’expérience ci-dessus. Dans l’état 1, un réservoir contient deux parties, à gauche un gaz composé d’atomes en mouvement, à droite le vide.

Dans l’état 2 on a ouvert le robinet, et le gaz occupe tout le volume disponible sous l’effet de l’agitation constante et aléatoire des molécules.

Deux constatations peuvent être faites :

• Il n’y a pas de réversibilité, car il est tout simplement quasi-impossible que les atomes en mouvement désordonné se retrouvent spontanément tous dans le réservoir de gauche !
• Dans l’état 1, on peut imaginer mettre à la place du robinet une petite turbine, qui produirait un travail quand le gaz lui passerait à travers pour remplir le compartiment 2. L’état 2 ne comporte plus cette potentialité, on dit que son entropie a augmenté .

On comprend que l’entropie mesure en quelque sorte le degré de répartition aléatoire, de désordre, des atomes d’un système. Plus un système est ordonné, plus son énergie utilisable sera importante, et plus il sera capable de produire un travail. Inversement plus le désordre des atomes est grand, moins on peut en tirer du travail.

Le physicien Carlo Rovelli a ainsi pu dire (1): « Pour avancer, le monde n’a pas besoin d’énergie. Il a besoin de basse entropie ».

Il a besoin en fait d’énergies ordonnées utilisables. Un peu plus loin, Rovelli poursuit :

Le physicien Ludwig Boltzmann, en 1877, va enfin donner la clé de l’entropie. La non réversibilité ne provient pas de son impossibilité, mais de sa probabilité considérée comme nulle à l’échelle de notre univers.

On va comprendre cet aspect en prenant un exemple très simplifié avec un jeu de 32 cartes. J’ai ordonné mon paquet de cartes pour avoir d’abord toutes les cartes rouges, dans n’importe quel ordre, puis les noires, également dans n’importe quel ordre. Je mélange mon jeu, et bien sûr les cartes se retrouvent dans un ordre aléatoire. Si je mélange successivement un grand nombre de fois mon jeu, il est théoriquement possible de retrouver par hasard une configuration rouge/noire comme à l’origine. Mais le calcul de cette probabilité donne un nombre infiniment petit (2). En pratique, avec un mélange des cartes toutes les secondes depuis le début de notre univers (environ 13,8 milliards d’années), il faudrait près de 29.000 fois cette durée pour y arriver.

Bon maintenant prenons un réservoir contenant non pas 32 mais des milliards d’atomes… L’impossibilité de la réversibilité vient de cette probabilité infiniment faible, nulle à l’échelle de notre univers.

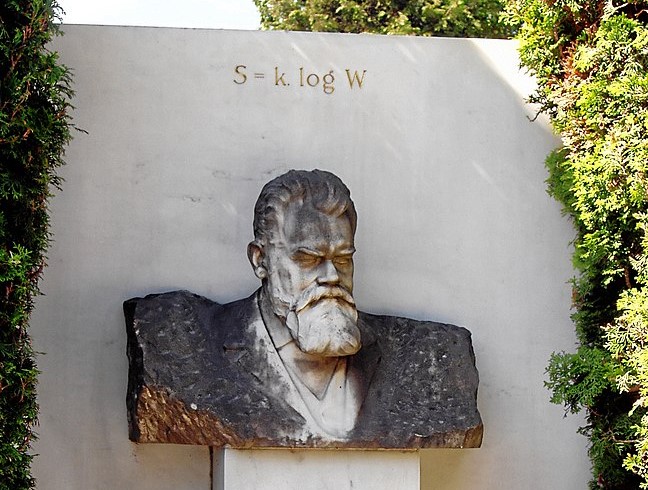
Ludwig Boltzmann est célèbre pour sa formule de l’entropie :  S = k . log W  , où k est la constante de Boltzmann et W le nombre de configurations microscopiques que peut prendre un système en équilibre. On peut avec cette formule calculer l’accroissement d’entropie d’un système qui évolue.

Boltzmann subira les railleries de ses pairs, alors majoritairement « anti-atomistes ». Il en souffrira énormément, et se suicidera en 1906.

Sa belle formule est gravée sur sa tombe.

–oo–oo

1. L’ordre du temps, p. 185 – Flammarion, 2019.
2. Le calcul utilise des factorielles : la probabilité est égale à (2 x 16 ! / 32 !) , soit de l’ordre de 10^{-22}.