Commençons par quelques questions simples, en apparence.
Il y a une infinité de nombres entiers (1, 2, 3, 4,…) puisqu’on peut compter sans jamais s’arrêter. Si on prend les nombres pairs (2, 4, 6, 8 …), ils sont aussi en nombre infini. Mais est-ce-que cet infini est 2 fois plus petit que celui des nombres entiers ?
Si j’ajoute deux infinis, par exemple l’ensemble des carrés (1², 2², 3², 4²,…) et l’ensemble des nombres impairs (1, 3, 5, 7, 9, 11,…), est-ce-que j’obtiens un infini plus grand ?
Ces questions ont-elles seulement un sens ?
L’Hôtel de Hilbert

Pour illustrer ces questions, le mathématicien Hilbert a imaginé un hôtel infini, pourvu d’un nombre de chambres infini numérotées 1, 2, 3, 4, 5 etc… On suppose que l’hôtel est plein, toutes les chambres sont occupées. Pourtant il pourra accueillir un nouveau client. Il suffira à l’hôtelier de demander à chaque client de déménager dans la chambre suivante : la 1 vers la 2, la 2 vers la 3, la 3 vers la 4… ce qui libérera la chambre N°1.
Mais voilà qu’un autobus infini amène une infinité de clients ! Pas de problème pour l’hôtelier, il va demander à la chambre 1 d’aller dans la 2, la 2 dans la 4, la 3 dans la 6 …soit en doublant le numéro de chaque chambre. Et ainsi une infinité de chambres se libère, elles ont toutes un numéro impair.
L’exemple de l’hôtel infini est amusant, mais il nous montre surtout la complexité du sujet des infinis.
Aleph zéro: \alef_0
Au XIXe siècle le génial mathématicien Georg Cantor permettra une avancée majeure sur ce sujet. Il introduisit la notion d’infini « dénombrable », baptisé \alef_0 (aleph zéro), l’infini des nombres entiers ou l’infini que l’on peut compter ou numéroter à l’aide des entiers. C’est le cas des infinis dont on a parlé et qui sont d’ordre \alef_0 : les nombres pairs ou impairs, l’ensemble des carrés etc.
Si l’on compare par exemple l’ensemble des nombres entiers et l’ensemble des carrés de ces nombres (1, 2, 9, 16, 25,…) on voit qu’il est possible d’associer à chaque nombre son carré (1 à 1, 2 à 4, 3 à 9, 4 à 16…). A chaque élément du premier infini il est possible d’associer un élément de l’autre infini et réciproquement, donc ces deux infinis ont la même taille, même si le premier infini contient la totalité du deuxième infini! Bref les manipulations des infinis sont très particulières.
Il n’existe pas d’infini plus petit que \alef_0 , mais il y en a des plus grands. Voyons cela.
Aleph un: \alef_1
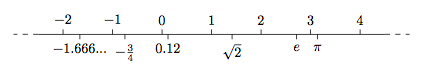
Considérons les nombres dits « réels », en gros tous ceux qu’on connaît, tous les points de la droite ci-dessus, y compris toutes les fractions, les racines, les puissances, ainsi que \pi par exemple. C’est un infini continu, puisqu’ entre deux points sur la droite, aussi proches qu’on veut, il y a une infinité d’autres points . Cantor a montré que cet infini est plus grand que \alef_0 , et l’a nommé \alef_1. Il n’est pas dénombrable car il est impossible d’associer chaque nombre réel à un nombre entier.
Des infinis plus grands

En 1900 à Paris se tint le 2e congrès international des mathématiciens. Hilbert y présenta une liste de 23 problèmes mathématiques toujours non résolus.
Le premier de ces problèmes était l’hypothèse du continu de Cantor, qui se posait aux mathématiciens depuis plusieurs décennies. Cantor faisait l’hypothèse qu’entre \alef_0 et \alef_1, il n’y avait pas d’autres infinis intermédiaires, qu’on passait du dénombrable au continu d’un seul coup, sans intermédiaire.
On a en fait démontré plusieurs décennies plus tard que le problème est indécidable. Il est impossible de démontrer ni que c’est vrai, ni que c’est faux.
Par contre il y a bien des infinis plus grands. Prenons un ensemble infini quelconque E. L’ensemble de toutes les parties de E est plus grand que E (1); cela paraît évident, mais ça se démontre. Ainsi il existe une hiérarchie infinie des infinis…
\alef_0{<}\alef_1{<}\alef_2{<}\alef_3 {...}–oo–oo–
- Par exemple si E = (1,2,3,4,5…) , l’ensemble de ses parties comprend (1), (2), (3), … (1,2), (1,3) , (1,4) … (2,3), (2,4), (2,5), …(1,2,3), (1,2,4)…