Au cours des siècles qui nous ont précédés, de plus en plus de calculs fastidieux sont nécessaires pour le développement des sciences physiques, astronomiques, financières … Prenez par exemple un simple calcul financier : un banquier a prêté une somme de 12.627 écus au taux de 6,5% pendant une période de 5 ans et 122 jours… Combien doit rembourser l’emprunteur ? Ou l’exemple d’un astronome qui doit vérifier par le calcul les relevés de l’orbite d’une planète…
Les premières machines à calculer mécaniques ne sont apparues qu’au début du 20e siècle, et les machines électroniques dans les années 1970. Aujourd’hui une simple calculette permet de faire ces calculs instantanément, au point qu’on a complétement oublié les siècles de calculs laborieux, au cours desquels on va perdre un temps fou pour faire les calculs, vérifier qu’il n’y a pas d’erreurs, recommencer, et ça ne fera qu’empirer avec le développement des sciences…
Il devenait urgent que des mathématiciens trouvent des solutions, d’abord pour faciliter les multiplications de grands nombres, mais aussi pour calculer les puissances, racines et autres. C’est ce que Neper, mathématicien écossais, fera en 1614.
Transformer une multiplication en addition
Archimède, au 3e siècle avant J.-C., savait que pour multiplier des puissances, on ajoute les exposants : a^n x a^m = a^{n+m}
Par exemple avec a = 10 ,
10^3 x 10^4 = 10^{3+4} = (10x10x10) x (10x10x10x10) = 10x10x10x10x10x10x10 = 10^7.
Dans le tableau qui suit, pour multiplier 1.000 par 10.000, on ajoute 3 + 4, et on lit le résultat devant le chiffre 7.

On a pris a = 10 par simplicité, mais on peut tout aussi bien prendre une autre valeur. Construisons le même tableau avec a = 2 par exemple :

Si je veux calculer 64 x 128, il me suffit d’ajouter ici aussi les exposants respectifs 6 et 7, soit 13, pour lire la réponse 8192.
Neper généralisera ce principe en appelant logarithme l’exposant, et en posant la relation fondamentale :
log ( A x B ) = log A + log B
Soit avec notre exemple : log ( 64 x 128 ) = log 64 + log 128 = 6 + 7 = 13 = log (8192)
On a bien transformé une multiplication en addition ! Mais pour que ce soit utile, il nous faut un tableau complet qui donne les logarithmes de tous les nombres possibles, et pas seulement ceux des tableaux précédents, 64, 128, 8192 …
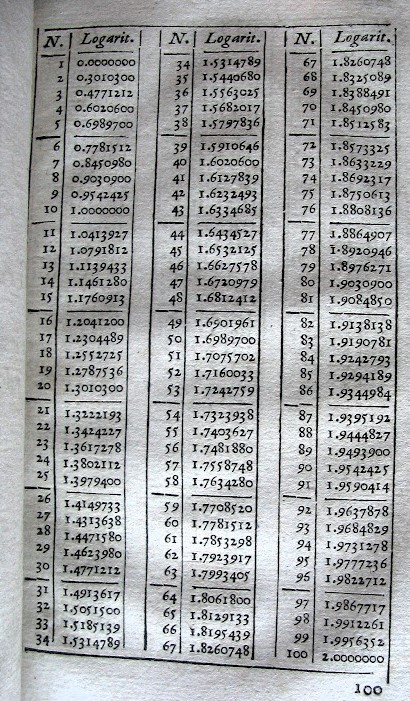
C’est ce qu’a publié Neper, sa table de logarithmes, avec la base a = 10 plus facile à manier que la base 2. Par exemple on trouve dans la table ci-contre le logarithme de 87, valeur comprise entre 10 et 100 dont le logarithme est donc compris entre 1 et 2 : 1,9395192.
On ne doit pas être étonné par un logarithme, donc un exposant, qui n’est pas un nombre entier. On sait en fait utiliser de tels exposants, par exemple:
\sqrt[2]{10} = 10^{1/2}\to de logarithme ½ = 0,5
\sqrt[4]{1000} = 10^{3/4}\to de logarithme ¾ = 0,75
Les tables de log
Utilisons les deux exemples précédents et plaçons-les sur un axe :
log ( \sqrt[2]{10} ) = log ( 3,16228 ) = 0,5
log ( \sqrt[4]{1000} ) = log ( 5,62341 ) = 0,75
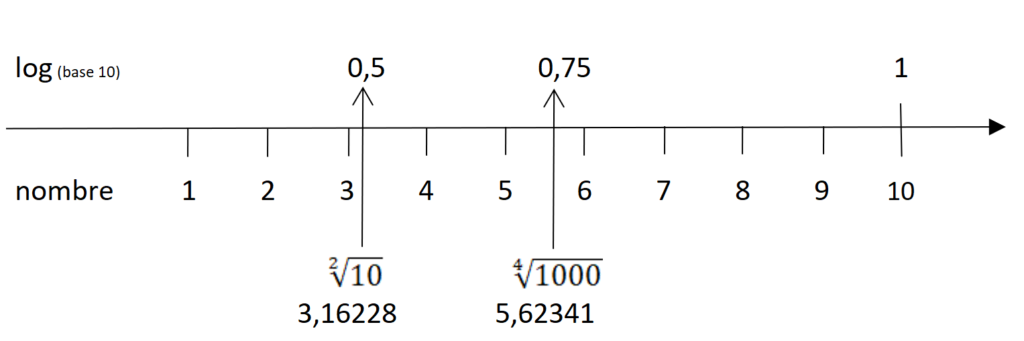
On voit qu’en généralisant ce type de calcul de multiple fois, puis par interpolation linéaire entre tous ces nombres, on peut construire des tables complètes avec les logarithmes de milliers de nombre entiers successifs, par exemple de 1 à 100.000.
Des calculs très simplifiés
Outre les multiplications des grands nombres qui deviennent de simples additions, beaucoup d’autre calculs deviennent très faciles, notamment grâce à la formule suivante :

log ( A^b ) = b . log (A )
Calculons par exemple : \sqrt[3]{8796}
log ( \sqrt[3]{8796} ) = log( 8796^{1/3} ) = 1/3 . log (8796) = 1,31476
d’où la réponse approchée lue dans la table de log : 20,6425 .
Autre exemple : 6,7542^6
log ( 6,7542^6 ) = 6 . log(67542/10000) = 6 . [ log (67542) – log(10000) ]
= 6 . (4,829574 – 4) = 4,977444 , ce qui correspond à 94.939 en valeur approchée.
Voilà comment des calculs affreusement longs deviennent d’une grande facilité.
–oo–oo–