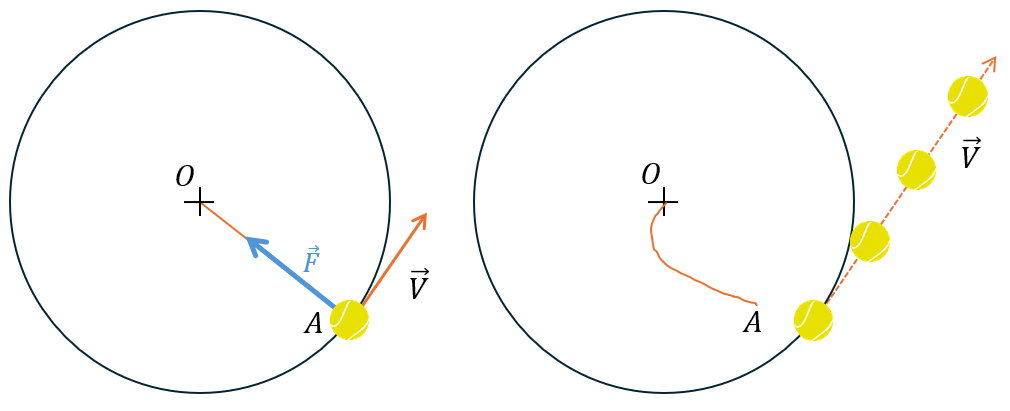
Ce billet et les suivants abordent les forces en présence lorsque des corps décrivent une trajectoire courbe, ‘tournent” : force centripète, centrifuge, force de Coriolis, gyroscope. Commençons par les bases de cette mécanique: notion de référentiel et lois du mouvement de Newton.

Dans quel repère es-tu ?

Pour étudier le mouvement d’un corps, sa position et sa vitesse dans le temps, on a besoin de se repérer par rapport à un référentiel. Dans l’exemple classique du train, si je suis assis à la place 25 du wagon 4, j’ai par rapport au train une position bien définie 25-4 et une vitesse nulle, alors que par rapport disons à la voie ferrée, ma position varie en permanence et ma vitesse est égale à celle du train.

Le choix d’un référentiel dépend de l’aspect pratique de l’étude qu’on mène : référentiel lié à la terre  par exemple ou référentiel héliocentrique lié à notre système solaire (centré sur le soleil et dont les axes pointent vers trois étoiles lointaines considérées comme fixes). Position et vitesse ne seront pas les mêmes du fait de la rotation de la terre sur elle-même et autour du soleil, mais bien sûr la trajectoire du corps est inchangée.

Référentiels Galiléens et loi d’inertie

Outre les position et vitesse du corps, l’étude de son mouvement nécessite de connaître les lois physiques qui s’appliquent. Newton a énoncé en 1687 les lois universelles du mouvement, base fondamentale de la Mécanique :

1^ère loi : un corps soumis à une force nulle est immobile ou en mouvement uniforme rectiligne.

Cette loi générale peut paraît évidente (dans l’espace, un objet qui n’est  soumis à aucune force continuera sa route rectiligne à vitesse constante éternellement), mais il faut ajouter que Newton la concevait dans un espace à 3 dimensions absolu, immuable, celui qu’on a naturellement en tête d’ailleurs.

Aujourd’hui, on sait qu’il n’existe pas d’espace absolu par rapport auquel on peut définir un mouvement (1). On a donné le nom de « Galiléen » à tout espace ou référentiel dans lequel la première loi de Newton est vraie, au contraire d’un référentiel accéléré ou en rotation dans lequel elle ne s’applique pas.

On montre facilement que les référentiels Galiléens ont une propriété fondamentale :  si un référentiel R1 est Galiléen, un autre référentiel R2 en mouvement rectiligne uniforme par rapport à R1 sera lui aussi Galiléen.

Le référentiel héliocentrique dont on a parlé plus haut peut être considéré en première approximation comme Galiléen, mais ce n’est  pas le cas d’un référentiel lié à la terre puisqu’elle tourne.

Ça tourne… la force centripète

Reprenons l’exemple de la fronde qui tourne autour de O. Entre deux points A et B, notons \overrightarrow{V1} et \overrightarrow{V2} son vecteur vitesse d’intensité constante V.

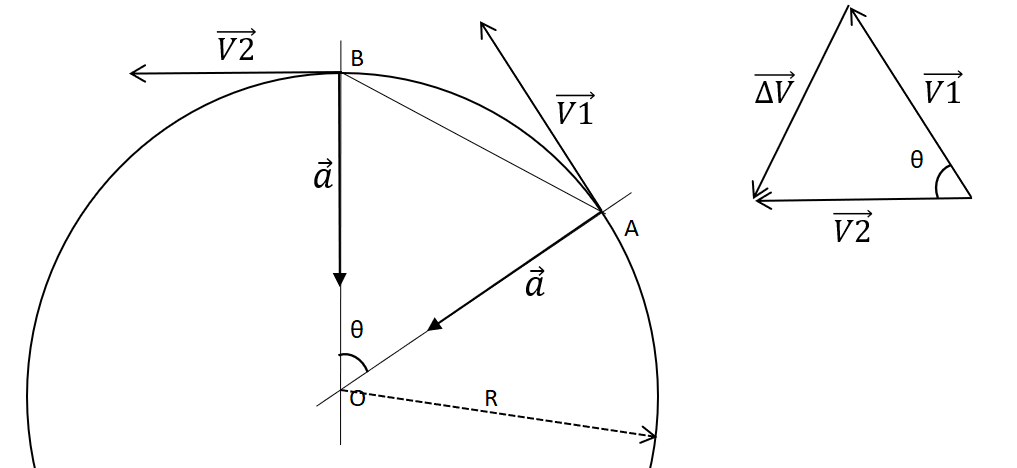
En posant la variation du vecteur vitesse \overrightarrow{\Delta V}=\overrightarrow{V2}-\overrightarrow{V1} on voit que le corps en B est animé de la vitesse \overrightarrow{V2}= \overrightarrow{V1}+ \overrightarrow{\Delta V} , c’est-à-dire qu’à la vitesse \overrightarrow{V1}  en A s’ajoute \overrightarrow{\Delta V}  , vitesse dirigée vers le centre, celle qui contraint l’objet à rester sur sa trajectoire circulaire.

Le triangle formé par les vecteurs \overrightarrow{V1}  et \overrightarrow{V2}  est semblable au triangle OAB et donc on peut écrire :  ΔV / V = AB / R .

Si l’angle θ  formé par nos deux rayons OA et OB est de plus en plus petit, le segment AB se confond avec l’arc de cercle AB,  parcouru en un temps Δt . On a alors :

AB = V . Δt  

ΔV / V = AB / R = V . Δt / R

ΔV / Δt = V² / R

Avec Δt infiniment petit, noté dt :

dV / dt = V² / R  ,

dV / dt   , dérivée de la vitesse par rapport au temps, représentant l’accélération centripète notée  aussi \overrightarrow{a}.

Pour qu’un corps soit en rotation uniforme, il doit être soumis à tout instant à une accélération centripète  d’intensité  a = V² / R .

Newton a énoncé une autre loi universelle du mouvement :

2^e loi : un corps de masse m soumis à une force \overrightarrow{F} est doté d’une accélération \overrightarrow{a}  telle que: \overrightarrow{F}=m.\overrightarrow{a}  .

L’intensité de la force centripète est donc : F = m . V²/R

La vitesse V et la vitesse de rotation en radian/seconde  ω sont liées par V = ω . R , ce qui donne :

Force centripète F = m . V² / R = m . ω² . R

–oo–oo–

1. Einstein en 1905 élabore sa théorie de la Relativité qui réfute en particulier l’idée d’espace absolu. Tous les espaces Galiléens sont équivalents, rien ne permet de distinguer l’un d’entre eux comme étant la référence des autres.