La force centripète et la pseudo-force centrifuge vues dans les billets précédents s’appliquent sur la terre, puisqu’elle tourne.
Sur la terre
Dans le référentiel lié à notre terre en rotation, un corps en un point A (voir les schémas ci-dessous) sera soumis à une pseudo-force centrifuge \overrightarrow{F} située dans un plan perpendiculaire à l’axe des pôles, et pas à la « verticale » du lieu comme le poids.
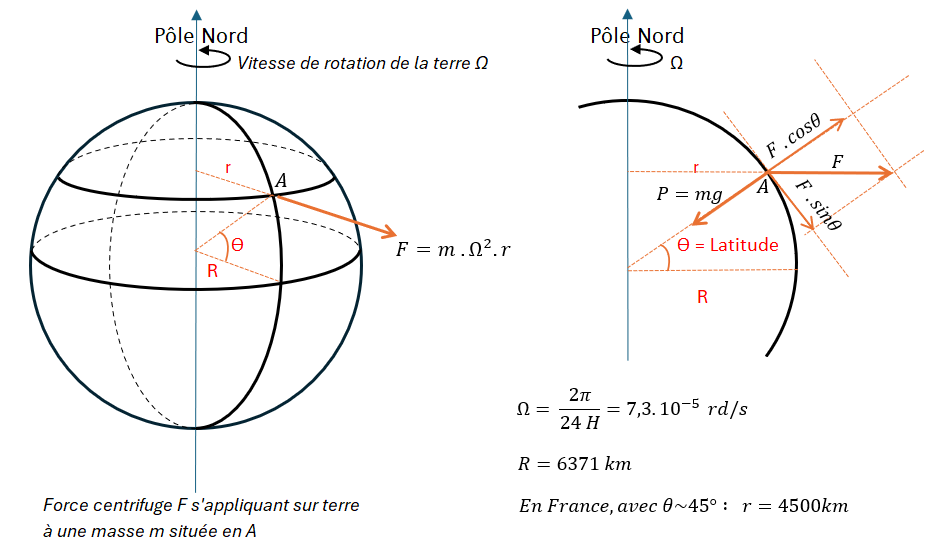
Décomposons \overrightarrow{F} en ses composantes « verticale » et « horizontale », et calculons l’ordre de grandeur de ces composantes pour une masse de 1.000 kg par exemple, de poids 1.000 x 9,81 = 9810 N, située en France, soit avec ϴ ~ 45° environ :
F.cosϴ = F.sinϴ = m . Ω² . r . \sqrt{2}/2 = 17 N , soit 0,17% du poids de la masse m.
Verticalement le poids est allégé de 0,17% , ce qui est pris en compte dans les valeurs de l’accélération de la pesanteur g qui dépendent (faiblement) de la latitude. Horizontalement, le corps en A est soumis également à une petite force de 17N, beaucoup plus faible que son poids, et peu sensible car contrebalancée par les frottements du sol.
En mouvement sur la Terre
Si maintenant le corps n’est plus fixe mais en mouvement avec une vitesse \overrightarrow{V} , donc libéré des frottements du sol, sa vitesse s’ajoutera vectoriellement à la vitesse due à la rotation de la terre, et il subira les effets de la pseudo-force centrifuge. L’étude exhaustive de ces effets fait appel mathématiquement au produit vectoriel que nous n’abordons pas ici.
Sur le terrain, on remarquera un phénomène étonnant, parfaitement illustré dans cette vidéo (1) :

L’objet rouge une fois lancé, libre de toute force, poursuit sa course en ligne droite (rouge) dans un repère Galiléen, c’est la 1e loi de Newton. Mais pour moi, qui suis sur le point jaune attaché à mon repère tournant, j’ai l’illusion d’une trajectoire courbe. C’est par exemple bien ce que je ressens si je marche sur un manège qui tourne…
Dans le repère tournant de la Terre, les physiciens ont inventé une 2e pseudo-force, la force de Coriolis, qui explique la déviation de la trajectoire d’un objet en mouvement sur sa droite dans l’hémisphère nord, et vers la gauche dans l’hémisphère sud.
Un cas simplifié très illustratif va nous permettre d’y voir plus clair…
Force de Coriolis
Par simplification supposons qu’un corps est en mouvement vers l’est, c’est-à-dire que sa vitesse s’ajoute à celle de la rotation de la terre (2).
Il est animé d’une vitesse V, à la latitude ϴ , ce qui correspond à une vitesse de rotation propre de ω = V/r . Sa vitesse de rotation totale est donc (Ω + ω) , et la pseudo-force centrifuge qui s’applique devient :
F = m . (Ω + ω)² . r = m . ( Ω²r + ω²r + 2Ωωr )
Avec les mêmes hypothèses que précédemment, et pour fixer les idées avec V=100 km/h, on a pour les trois termes :
- mΩ²r = 24N force centrifuge due à la rotation de la terre (§ précédent)
- mω²r = mV²/r = 0,2 N appelée « Force d’entraînement »
- 2mΩωr = 2mΩV = 4,1 N appelée « Force de Coriolis »
En décomposant la force de Coriolis comme on l’a fait au paragraphe précédent, la force « horizontale » est une force dirigée vers la droite du mouvement (dans l’hémisphère Nord) :
F Coriolis = 2 m Ω V . sinϴ
Bien que faible, pour des masses ou des vitesses plus importantes cette force va faire dévier les trajectoires de façon significatives, et expliquer le sens de rotation des cyclones par exemple.
–oo—oo–
- Timo van Neerden, « La force de Coriolis et les tornades dans vos éviers», Couleur-Science, 18 septembre 2013, https://couleur-science.eu/?d=1f020d–la-force-de-coriolis-et-les-tornades-dans-vos-eviers
- Voir une étude fouillée sur ces sujets : http://francois.lonchamp.free.fr/Coriolis/Force%20de%20Coriolis.html