Cette vidéo est vraiment étonnante! Lorsqu’on coupe une des deux ficelles, on s’attend à voir la roue de bicyclette tomber et pendre au bout de la deuxième ficelle. Mais ça ne se passe pas du tout comme prévu:
- l’axe de la roue reste (à peu près) horizontal
- et le plan de la roue se met en rotation
Pour expliquer cette expérience tout à fait contre-intuitive, il nous faut d’abord aborder la notion de quantité de mouvement circulaire d’un objet en rotation autour d’un axe.
Lois de conservation
On a vu dans les billets précédents qu’un corps de masse m, qui n’est soumis à aucune force extérieure, a une accélération nulle, c’est la 2e loi de Newton. Sa vitesse est donc constante en intensité et en direction, et sa quantité de mouvement \overrightarrow{P} = m . \overrightarrow{V} également. Sans force extérieure ni frottement, le corps va poursuivre sa trajectoire rectiligne à vitesse constante indéfiniment.
De même, un corps en rotation autour d’un axe Δ , qui n’est soumis à aucune force (ou couple) extérieur, va poursuivre sa rotation indéfiniment autour de Δ . Sa quantité de mouvement circulaire et son axe de rotation sont constants, c’est également une loi fondamentale(1).
Cette conservation de l’axe de rotation est bien cohérente avec notre vidéo dans laquelle l’axe de la roue de bicyclette reste étonnamment horizontal lorsque la ficelle est coupée.
Précession
Dans cette expérience, la roue de bicyclette est en réalité soumise à la force de son poids, qu’on va maintenant considérer.
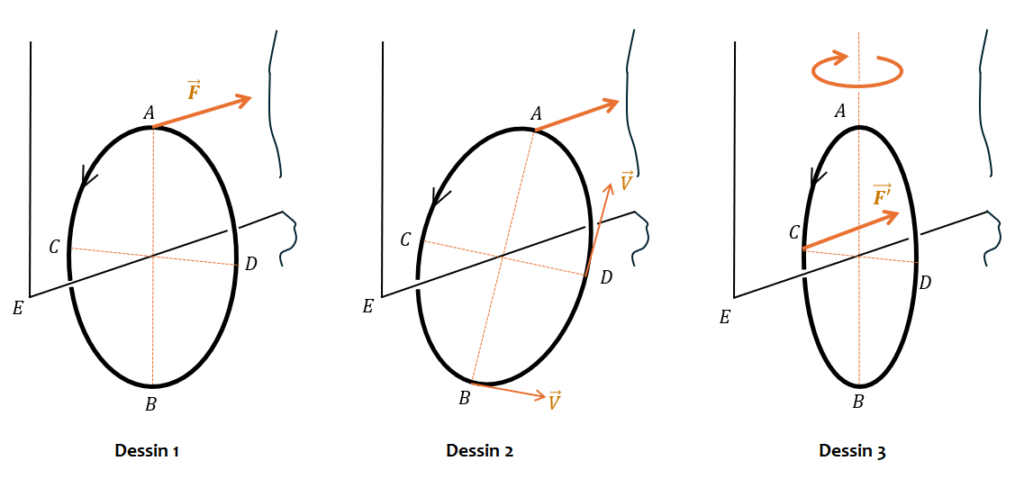
Le poids de la roue crée un couple qui tend à faire pivoter son axe autour du point E, ce qui est équivalent à l’application d’une force \overrightarrow{F} (dessin N°1). Sous l’action de cette force, la roue aurait tendance à s’incliner comme le montre le dessin N°2, ce qui induirait que les vecteurs vitesse \overrightarrow{V} des portions de roue situées en C et D auraient tendance à faire pivoter le plan de la roue dans le sens indiqué sur le dessin N°3. En revanche les vecteurs vitesse \overrightarrow{V} des portions de roue situées en A et B n’ont pas cette influence, étant parallèles à l’axe CD.
En définitive, lorsqu’on applique une force à un corps en rotation, tout se passe comme si ce corps était soumis à une force située à 90° dans le sens de la rotation. Et c’est bien ce que la vidéo nous a montré, de façon ici aussi contre intuitive !

Le changement d’orientation de l’axe de rotation, ici d’un gyroscope, dû à l’action d’un couple ou d’une force extérieure (ici le poids du gyroscope), s’appelle la précession.
–oo–oo–
- La conservation de la quantité de mouvement circulaire est en fait définie à partir du”moment cinétique” ou “moment angulaire”, produit vectoriel mathématique.