Tout le monde, enfin presque, connaît le théorème de Pythagore. Disons que ça fait plus de 2000 ans qu’on le connaît tout de même !

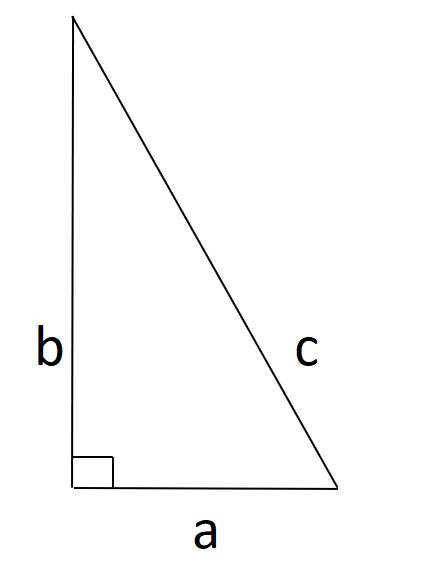
Ce théorème dit que, dans un triangle rectangle, le carré de l’hypoténuse (le plus grand côté) est égal à la somme des carrés des 2 autres côtés :

c² = a² + b²

On s’en sert quand on veut tracer un angle droit, sur un terrain par exemple. On va construire un triangle avec 3 côtés qui font respectivement 3m, 4m et 5m de longueur, et on obtient un angle droit.

Car     3² + 4² = 5² ,     ou     9 + 16 = 25.

On trouve de multiples démonstrations de ce théorème, mais il y en a une que j’aime beaucoup tant elle est astucieuse.

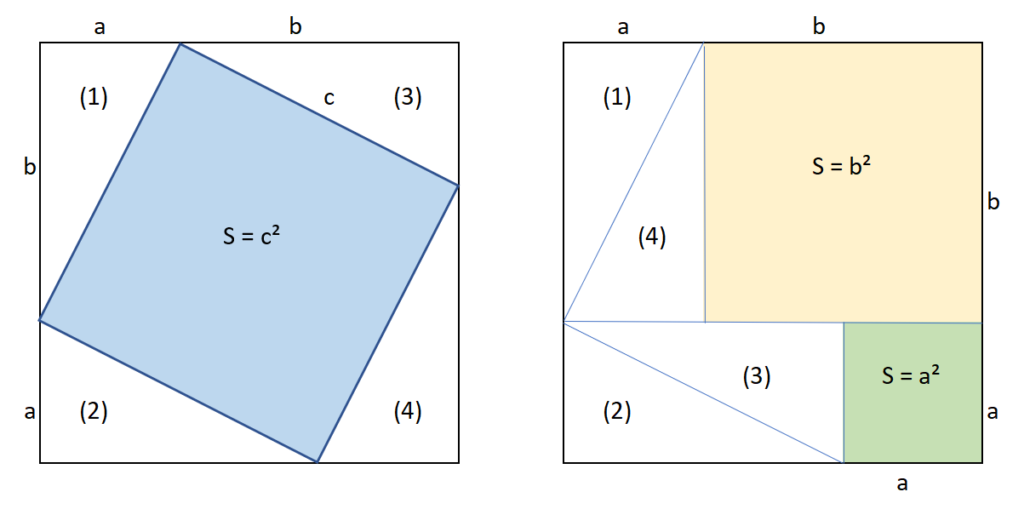
A gauche j’ai un grand carré de côté ( a + b ) . Il est composé de 4 triangles rectangles notés (1), (2), (3) et (4), et du carré bleu de côté c et de surface c².

A droite j’ai le même grand carré. Il est composé des 4 mêmes triangles rectangles (1), (2), (3) et (4), complété par le carré jaune de surface b² et du carré vert de surface a².

Les deux  grands carrés de gauche et de droite étant égaux, on a : c² = a² + b²  .

Bien joué, non ?

–oo–oo–